Mechanical properties of bone
Introduction
Although an organic material, bone can often be considered in the same way as man-made engineering materials. However, due to the nature of its synthesis it is likely to show more variation in measured properties than typical engineering materials. Factors include:
- Age
- Gender
- Location in the body
- Temperature
- Mineral content
- Amount of water present
- Disease, e.g. osteoporosis
These variables can to an extent be dependent on each other. For example, the mineral content will vary according to the bone’s location in the body, and with the age of the patient.
As humans age, their bones typically become less dense and the strength of these bones decreases, meaning they are more susceptible to fracture. Osteoporosis is a disease involving a marked decrease in bone mass, and it is most often found in post-menopausal women.
These variables mean that there is a range of measured properties for bone, and so values given in tables will always be an average, with quite a considerable spread possible in the data.
In addition, the anisotropic structure of bone means that its mechanical properties must be considered in two orthogonal directions:
- Longitudinal, i.e. parallel to osteon alignment. This is the usual direction of loading
- Transverse, i.e. at right-angles to the long axis of the bone
Modulus
Bone can be considered to consist primarily of collagen fibres and an inorganic matrix, and so on a simple level it can be analysed as a fibre composite.
Composites are materials that are composed of two or more different components. They are commonly used in engineering and industry where the combination of the two materials creates a composite with properties that are superior to those of the individual components.
The Young’s Modulus of aligned fibre composites can be calculated using the Rule of Mixtures and the Inverse Rule of Mixtures for loading parallel and perpendicular to the fibres respectively.
RULE OF MIXTURES
Eax = f Ef + (1 - f) Em
INVERSE RULE OF MIXTURES
\( E_{ax} = \left[ {\frac{f}{{E_f }} + \frac{{\left( {1 - f} \right)}}{{E_m }}} \right]^{ - 1} \)
Where
Ef = Young’s Modulus of fibres
Em = Young’s modulus of matrix
Eax, Etrans = Young’s Modulus of composite in axial and transverse directions
f= volume fraction of fibres
For the full derivation of these rules, click here.
These formulae predict that the composite will be stiffer in the axial direction than the transverse, so cortical bone will be stiffer in the direction parallel to the osteons (i.e. parallel to the long axis of the bone).
The chart below shows calculated values for the Young's Modulus of bone in both the longitudinal and transverse directions, for a range of fibre volume fractions, as well as the actual values.
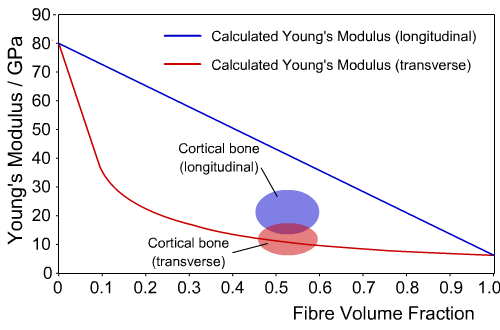
Calculated and experimental values of Young’s Modulus for cortical bone
We can see that for the transverse direction, the composite model closely agrees with experimental values. However, in the longitudinal direction the difference is large, indicating the model does not give an accurate picture of the behaviour of bone.
This difference occurs because the composite model of the microstructure of bone is highly simplified, since the collagen fibres are not aligned parallel to the axis of the osteons, and the bone mineral exists as discrete crystals, rather than forming a continuous matrix.
A better approximation would be to model bone as a two level composite. One level is provided by hydroxyapatite-reinforced collagen in a single osteon, and the second level is obtained by the approximately hexagonal packing of osteons in a matrix of interstitial bone.
The actual values for the Young’s modulus of bone, compared to collagen and hydroxyapatite, are shown in the table below. The measured value of Young’s Modulus also depends on temperature, decreasing with an increase in temperature, and the strain rate, increasing in value with an increase in strain rate.
Material |
Young’s Modulus, E (GPa) |
Collagen (dry) |
6 |
Bone mineral (Hydroxyapatite) |
80 |
Cortical bone, longitudinal |
11-21 |
Cortical bone, transverse |
5-13 |
Tensile and Compressive Strength
As mentioned previously, bones such as the femur are subjected to bending moments during normal loading. These create both tensile and compressive stresses in different regions of the bone.
There is a large variation in measured values of both the tensile and compressive strength of bone. Different bones in the body need to support different forces, so there is a large variation in strength between them. Additionally, age is an important factor, with strength often decreasing as a person gets older.
|
Longitudinal direction |
Transverse direction |
Tensile strength (MPa) |
60-70 |
~50 |
Compressive strength (MPa) |
70-280 |
~50 |
Elasticity
Bone mineral is a ceramic material and exhibits normal Hookean elastic behaviour, i.e. a linear stress-strain relationship. In contrast, collagen is a polymer that exhibits a J-shaped stress-strain curve. (See the TLP Elasticity in Biological Materials.
Typical stress-strain curves for compact bone, tested in tension or compression in the wet condition, are approximately a straight line. Bone generally has a maximum total elongation of only 0.5 - 3%, and therefore is classified as a brittle rather than a ductile solid.
Fracture Toughness
In contrast to the findings for tensile and compressive strength and modulus, the values of toughness in the transverse direction are generally higher than those in the longitudinal direction. This is due to the presence of the cement lines in the microstructure. These are narrow regions around the outermost lamellae in the osteons, and they form the weakest constituent of bone. Crack propagation parallel to the osteons can occur much more easily through these regions and this significantly decreases the fracture toughness of cortical bone in the longitudinal direction. If a crack is propagating perpendicular to an osteon it will change direction when it reaches a cement line, thus blunting the crack. This is illustrated in the animation below.
As a result, although bone is classified as a brittle material (with the major component being mineral), its toughness is excellent. Bone’s fracture energy, Gc, is approximately 1.5 kJ m-2, which is comparable to steel at low temperatures and wood when measured parallel to the grain. This is much tougher than man-made ceramics due to the presence of the collagen fibres in bone. Since the stress-strain curves for loading and unloading are different the elasticity is therefore time-dependent, a common feature of fibrous proteins. For a full discussion of this see the TLP Elasticity in Biological Materials.

