Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Introduction To Dislocations Slip via dislocation motion
Introduction To Dislocations AimsBefore you startIntroductionDislocations in 2DBubble raftDislocation motionDislocation glideDislocations in 3DObserving dislocationsSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Slip via dislocation motion

It is possible to estimate the stress required for slip by movement of lattice planes past one another (i.e. in a perfect crystal) and for slip by dislocation motion.

Stress required for slip in a perfect crystal

One can estimate the shear stress required to cause slip in a perfect crystal as follows. Imagine two close-packed planes with separation h and interatomic distance b. On application of a shear stress τ, the top plane moves a distance u with respect to the bottom plane as shown in the diagram.

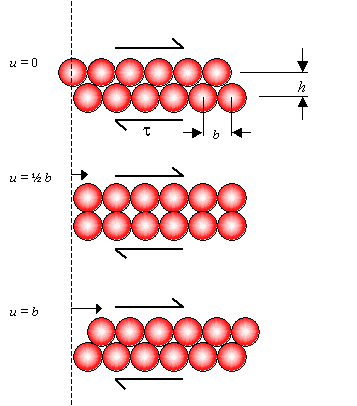
Diagram illustrating slip by movement of lattice planes

The shear stress τ needed for slip to proceed in this way is zero when u = 0, u = ½ b and u = b etc. As a first approximation we assume that τ varies sinusoidally with u, then a suitable form for τ is:

$$\tau = {\tau _{crit}}\sin {{2\pi u} \over b}$$

where τcrit is a constant that equals the shear stress that must be applied to move one close-packed plane continuously over the next, and hence corresponds to the maximum value of τ. This maximum occurs when u = b/4.

τ is related to the shear strain γ by the shear modulus, G:

$$\tau = G\gamma $$

and the shear strain angle γ is given by

$$\gamma = {u \over h}$$

It is now possible to make the assumption that the ratio u/b is small since the macroscopic slip is the result of a small amount of slip on each plane, rather than a large amount on one plane. This simplifies the expression since sin x ~ x.

Combining equations [1] and [3],

$$\tau = {\tau _{crit}}\sin {{2\pi u} \over b} = 2\pi {\tau _{crit}}{{h\gamma } \over b}$$

Rearranging equation [2] and substituting,

$${\tau \over \gamma } = G = {{2\pi {\tau _{crit}}h} \over b}$$

hence

$${\tau _{crit}} = {{Gb} \over {2\pi h}}$$

For close-packed spheres, b/h = 2/31/2, which gives

$${\tau _{crit}} = {{Gb} \over {\pi \sqrt 3 }} \approx {G \over 5}$$

Stress required for slip by means of dislocation motion

When a dislocation line moves through a crystal, the interatomic forces across the slip plane are overcome in a series of local movements, rather than breaking all of the atomic bonds across the slip plane at once as would occur in a perfect lattice. The stress needed to drive a dislocation through a crystal continuously is called the Peierls-Nabarro stress, τp. Calculation of τp is difficult, and it depends on the ratio of the dislocation width w to the magnitude of the Burgers vector b. One simple model gives:

$${\tau _p} = 3G\exp \left( { - {{2\pi w} \over b}} \right)$$

Setting w = b, which is the minimum reasonable width for a dislocation, and therefore will give the maximum τp, reduces equation [6] to:

$${\tau _p} = 3G\exp ( - 2\pi ) \approx {G \over {180}}$$

This approximate calculation shows that the Peierls-Nabarro stress to move a dislocation through a lattice (equation [7]) is orders of magnitude less than the stress required to cause slip in a perfect lattice (equation [5]). Therefore it follows that slip occurs by dislocation motion when dislocations are present in the lattice.

PreviousNext