Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Slip in Single Crystals Slip geometry: the critical resolved shear stress
Slip in Single Crystals AimsBefore you startIntroductionSlip geometry: the critical resolved shear stressGeometry during slipSlip in HCP metals 1: slip systemsSlip in HCP metals 2: application of Schmid's LawSlip in HCP metals 3: calculation of forcesSlip in HCP metals 4: observing slip in cadmiumVideo clips of slip in a single cadmium crystalExercise: Determination of the critical resolved shear stress for slip in cadmiumSlip in CCP metalsSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Slip geometry: the critical resolved shear stress

Slip occurs by dislocation motion. To move dislocations, a certain stress must be applied to overcome the resistance to dislocation motion. This is discussed further in the Introduction to dislocations package on this site.

It is observed experimentally that slip occurs when the shear stress acting in the slip direction on the slip plane reaches some critical value. This critical shear stress is related to the stress required to move dislocations across the slip plane.

The tensile yield stress of a material is the applied stress required to start plastic deformation of the material under a tensile load. We want to relate the tensile stress applied to a sample to the shear stress that acts along the slip direction. This can be done as follows. Consider applying a tensile stress along the long axis of a cylindrical single crystal sample with cross-sectional area A:

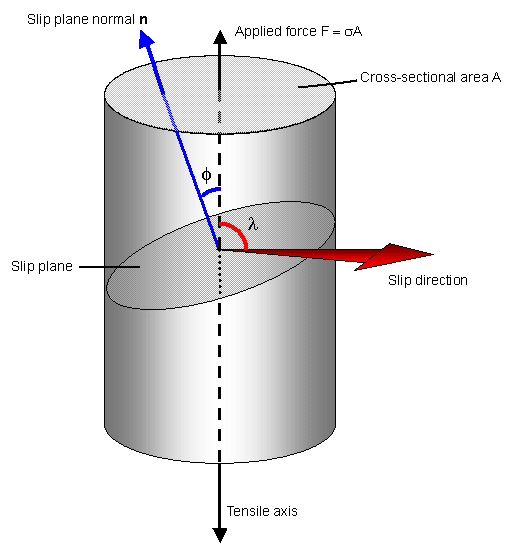
Diagram illustrating application of tensile stress along the long axis of a cylindrical single crystal sample

The applied force along the tensile axis is F = σA. If slip occurs on the slip plane shown in the diagram, with plane normal n, then the slip direction will lie in this plane. We can calculate the resolved shear stress acting parallel to the slip direction on the slip plane as follows.

The area of the slip plane is A/cosφ, where φ is the angle between the tensile axis and the slip plane normal.

The component of the axial force F that lies parallel to the slip direction is F cos λ. The resolved shear stress on the slip plane parallel to the slip direction is therefore given by:

\[{\tau _{\rm{R}}} = \frac{{{\rm{resolved}}\;{\rm{force}}\;{\rm{acting}}\;{\rm{on}}\;{\rm{slip}}\;{\rm{plane}}}}{{{\rm{area}}\;{\rm{of}}\;{\rm{slip}}\;{\rm{plane}}}} = \frac{{F\cos \lambda }}{{A/\cos \varphi }} = \frac{F}{A}\cos \varphi \cos \lambda \]

It is found that the value of τR at which slip occurs in a given material with specified dislocation density and purity is a constant, known as the critical resolved shear stress τC. This is Schmid's Law.

The quantity cos φ cos λ is called the Schmid factor. The tensile stress at which the crystal starts to slip is known as the yield stress σy, and corresponds to the quantity F/A in the above equation.

Symbolically, therefore, Schmid's Law can be written:

τC = σy cos φ cos λ

In a given crystal, there may be many available slip systems. As the tensile load is increased, the resolved shear stress on each system increases until eventually τC is reached on one system. The crystal begins to plastically deform by slip on this system, known as the primary slip system. The stress required to cause slip on the primary slip system is the yield stress of the single crystal. As the load is increased further, τC may be reached on other slip systems; these then begin to operate.

From Schmid's Law, it is apparent that the primary slip system will be the system with the greatest Schmid factor. It is possible to calculate the values of cos φ cos λ for every slip system and subsequently determine which slip system operates first. This can be time consuming, but for cubic crystal systems, the OILS rule and Diehl's rule provide quick routes to identifying the primary slip system.

PreviousNext