Constitutional Undercooling
It is actually rare to have a negative temperature gradient ahead of the interface, yet it is observed that dendrites are very hard to avoid in practice. This occurs because most materials in use have significant levels of impurities. The following animation shows how dendrites form in a binary alloy:
The situation can be analysed quantitatively to determine whether a dendritic growth front is likely. If we assume a steady state diffusion profile ahead of the interface (see page on Steady State Solidification), the concentration of solute at any distance, x’, ahead of the interface is given by:
\[C = {C_0} + \frac{{{C_0}\left( {1 - k} \right)}}{k}\exp \left( {\frac{{ - x}}{{{D_{\rm{L}}}/v}}} \right) \;\;\;\;\;\;(1)\]
The liquidus temperature, TL, on the phase diagram is dependent on the concentration of solute by the equation:
\[{T_{\rm{L}}} = {T_{\rm{m}}} + C\frac{{\partial {T_{\rm{L}}}}}{{\partial C}}\]
where Tm is the melting temperature of the pure substance, and ∂T / ∂x is the gradient of the liquidus on the phase diagram, which is usually negative if k < 1.
The graph of liquidus temperature against distance, has a profile like the one shown below:
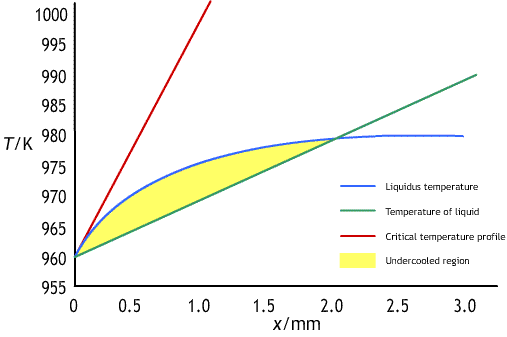
There will be an undercooled region ahead of the interface, in which a planar interface is unstable, if the temperature gradient, ∂T / ∂x, ahead of the interface is less than the gradient of the liquidus temperature at the interface. To maintain a planar interface the relationship below must hold:
\[\frac{{\partial T}}{{\partial x}} > {\left. {\frac{{\partial {T_{\rm{L}}}}}{{\partial x}}} \right|_{x = 0}}\]
which, by the chain rule becomes:
\[\frac{{\partial T}}{{\partial x}} > \frac{{\partial {T_{\rm{L}}}}}{{\partial C}}{\left. {\frac{{\partial C}}{{\partial x}}} \right|_{x = 0}}\]
By differentiating (1) with respect to x, and setting x = 0, we get:
\[{\left. {\frac{{\partial C}}{{\partial x}}} \right|_{x = 0}} = - \frac{{{C_0}}}{{{D_{\rm{L}}}/v}}\frac{{\left( {1 - k} \right)}}{k}\]
The critical gradient required to maintain a planar interface is given by:
\[{\frac{{\partial T}}{{\partial x}}_{{\rm{crit}}}} = - \frac{{{C_0}}}{{{D_{\rm{L}}}/v}}\frac{{\left( {1 - k} \right)}}{k}\frac{{\partial {T_{\rm{L}}}}}{{\partial C}}\]
For temperature gradients only slightly below the critical gradient, the planar interface will break down, but the trapping of solute partitioned between the primary dendrite arms prevents growth of secondary arms, and a cellular growth front evolves.
The simulation below allows you to predict the morphology of the solid growth in various systems.
The next simulation plots the liquidus temperature, in black, against distance, on the lower chart. This is calculated from the composition of the liquid, which is plotted on the upper chart. The simulation also plots a temperature profile in the liquid, in red. The gradient of this can be changed using the scrollbar labelled ∂T / ∂x. The upper limit of this gradient is 10000 K m-1, which is an approximate upper limit for gradients that can be practicably achieved. The critical gradient required to ensure a planar interface is plotted in green, and is also displayed in the box. The partition coefficient, k, the bulk concentration, C0, the diffusivity in the liquid DL, and the growth front velocity, v, can all be adjusted using the appropriate scrollbars.
Try adjusting the variables to see how the critical gradient, and the liquidus temperature profile change. Use the appropriate equations to justify the behaviour of the simulation.
You should note that in order to ensure a planar interface, the growth front velocities need to be quite low, of the order of 10s of microns per second. This is why it is often difficult to avoid dendritic growth in practical solidification.
In dendritic growth, most of the solute is ejected between the dendrite arms. The structure of the dendrites serves to prevent mixing with the rest of the liquid, so that the solute partitioning described earlier occurs over the length scale of the secondary dendrite arm spacing. This is known as microsegregation.

