Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Bending and Torsion of Beams Beam deflections from applied bending moments
Bending and Torsion of Beams AimsBefore you startIntroductionPole-vaultingBending moments and beam curvaturesMaximising the beam stiffnessBeam deflections from applied bending momentsTwisting moments (torques) and torsional stiffnessSpringsPlastic deformation during beam bendingSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Beam deflections from applied bending moments

As illustrated in the diagram below, the beam curvature, κ, is approximately equal to the second derivative (curvature) of the neutral axis line (dotted line in diagram)

\[\kappa = \frac{{{d^2}y}}{{d{x^2}}}\]

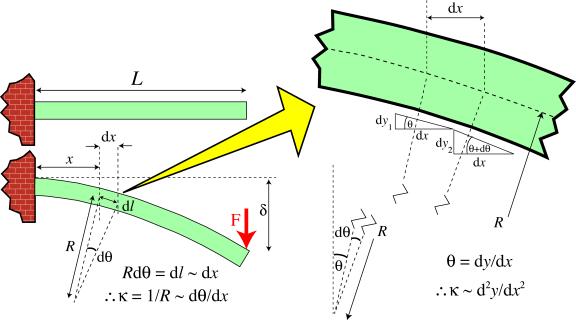
The approximation involved in equating beam curvature to the curvature of the neutral axis of a beam.

It follows that

\[M = \kappa EI = EI\frac{{{{\rm{d }}^2}y}}{{{\rm{d }}{x^2}}}\]

Since the moment at the section concerned can also be written, for a cantilever beam, as M = F (L - x)

it follows that

\[EI\frac{{{{\rm{d }}^2}y}}{{{\rm{d }}{x^2}}} = F\left( {L - x} \right)\]

This second order differential equation can be integrated (twice), with appropriate boundary conditions, to find the deflection of the beam at different points along its length. For a cantilever beam, this operation is shown below.

\[\begin{array}{l} EI\frac{{{\rm{d }}y}}{{{\rm{d }}x}} = FLx - \frac{{F{x^2}}}{2} + {C_1}\\ {\rm{at }}\;x = 0, \frac{{{\rm{d }}y}}{{{\rm{d }}x}} = 0, {\rm{thus\; }}{C_1} = 0 \end{array}\]

\[\begin{array}{l} EIy = \frac{{FL{x^2}}}{2} - \frac{{F{x^3}}}{6} + {C_2}\\ {\rm{at }}\;x = 0, y = 0, {\rm{thus\; }}{C_2} = 0 \end{array}\]

which can be rearranged to give

\[y = \frac{{F{x^2}}}{{6EI}}(3L - x)\]

For example, at the loaded end ( x = L ), this gives

\[\delta = \frac{{F{L^3}}}{{3EI}}\]

The corresponding operation for symmetrical 3-point bending can be seen by clicking here .

PreviousNext