Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Bending and Torsion of Beams Twisting moments (torques) and torsional stiffness
Bending and Torsion of Beams AimsBefore you startIntroductionPole-vaultingBending moments and beam curvaturesMaximising the beam stiffnessBeam deflections from applied bending momentsTwisting moments (torques) and torsional stiffnessSpringsPlastic deformation during beam bendingSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Twisting moments (torques) and torsional stiffness

Torsion is the twisting of a beam under the action of a torque(twisting moment). It is systematically applied to screws, nuts, axles, drive shafts etc, and is also generated more randomly under service conditions in car bodies, boat hulls, aircraft fuselages, bridges, springs and many other structures and components. A torque, T , has the same units (N m) as a bending moment, M . Both are the product of a force and a distance. In the case of a torque, the force is tangential and the distance is the radial distance between this tangent and the axis of rotation.

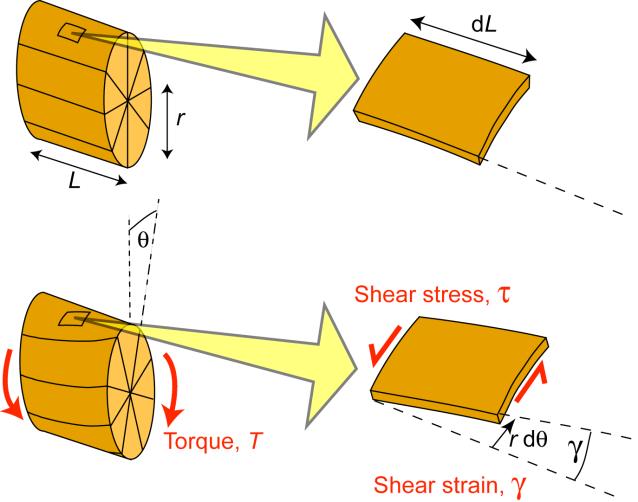
Torsion of a Cylindrical Bar

Torsion of a cylindrical bar is illustrated in the figure. It can be seen that the shear strain in an element of the bar is given by

\[\gamma = \frac{{r\;{\rm{d}}\theta }}{{{\rm{d}}L}}\]

This equation applies both at the surface of the bar, as shown, and also for any other radial location, using the appropriate value of r . Clearly, the shear strain varies linearly with r , from zero at the centre of the bar to a peak value at the free surface.

The shear stress, τ, at any radial location, is related to the shear strain by

\[\tau = G\gamma \]

where G is the shear modulus. It follows that

\[\tau = Gr\frac{{{\rm{d}}\theta }}{{{\rm{d}}L}}\]

The torque, T , can therefore be written as

\[T = \int\limits_A {{\rm{d}}T = } \int\limits_A {\tau \;r\;{\rm{d}}A} = \int\limits_A {G\;{r^2}\frac{{{\rm{d}}\theta }}{{{\rm{d}}L}}{\rm{d}}A} \]

As for the beam bending case, the geometrical integral is represented as a (polar) second moment of area

\[{I_{\rm{P}}} = \int\limits_A {{r^2}{\rm{d}}A} \]

For a solid cylinder of diameter w , this can be written as

\[{I_{\rm{P}}} = \int\limits_A {{r^2}} {\rm{d}}A = \int\limits_0^{d/2} {{r^2}2} \pi r\;{\rm{d}}r = \pi \left[ {\frac{{{r^4}}}{2}} \right]_0^{w/2} = \frac{{\pi {w^4}}}{{32}}\]

The torque is thus given by

\[T = G\;{I_{\rm{p}}}\frac{{{\rm{d}}\theta }}{{{\rm{d}}L}}\]

Comparing this equation with the corresponding one for beam bending

M = E I Κ

it can be seen that the torsional analogue for the curvature of a bent beam is the rate of twist along the length of the bar. This can be measured experimentally, although not quite so easily as a curvature (because the macroscopic shape of the bar does not actually change - at least when it is straight - see next page for an important example of a case when it is NOT straight).

PreviousNext