Derivation of the rule of mixtures and inverse rule of mixtures
Consider a simple model of a continuous fibre composite in which the fibres and matrix are each represented as solid blocks with volumes proportional to their relative abundance in the composite.
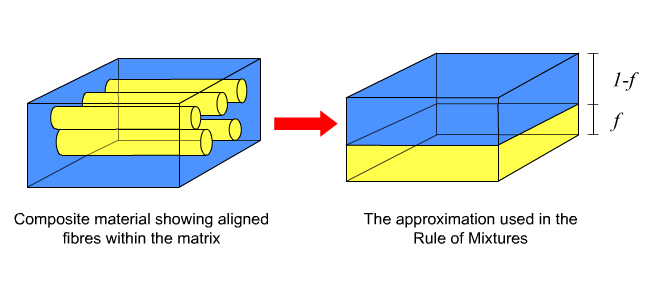
Axial loading
Now, if we consider a force applied in a direction parallel to the long axes of the fibres, the strain on the fibres must equal the strain on the matrix. These strains are in turn equal to the total strain on the composite,
εax = εf = εm (i)
As \(\varepsilon = \)\(\frac{\sigma }{E} \) (ii)
\[ \varepsilon _{ax} = \varepsilon _f = \frac{{\sigma _f }}{{E_f }} = \varepsilon _m = \frac{{\sigma _m }}{{E_m }} \tag{iii} \]As stress is force per unit area, it can also be seen that the overall stress,
σax = f σf + (1 - f) σm (iv)
Combining equations (iii) and (iv) gives an expression for the axial Young’s Modulus
Eax εax = f Ef εf + (1 - f) Em εm (v)
and since εax = εf = εm
Eax = f Ef + (1 - f) Em (vi)
This is known as the Rule of Mixtures.
Transverse loading
A similar approach can also be used to find an expression for transverse stiffness if the load is applied perpendicular to the fibres.
In this case an equal stress assumption is made,
σtrans = σf = Ef εf = σf = Em εm (vi)
The overall strain in the composite is:
εtrans = f εf + (1 - f) εm (viii)
The transverse modulus of the composite is then given by:
\[ E_{trans.} = \frac{{\sigma _{trans} }}{{\varepsilon _{trans} }} = \frac{{\sigma _f }}{{f\varepsilon _f + (1 - f)\varepsilon _m }} = \left[ {\frac{f}{{E_f }} + \frac{{(1 - f)}}{{E_m }}} \right]^{ - 1} \]
This is known as the Inverse Rule of Mixtures. It is not as accurate as the Rule of Mixtures because the equal stress assumption is not entirely valid – parts of the matrix will be shielded from stress by the fibres.

