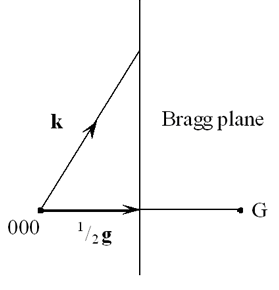
Bragg planes and Brillouin zone construction
The construction of Bragg Planes in the context of Brillouin zones can be understood by considering Bragg’s Law
λ = 2dsinθ
where θ is the angle between the incident radiation and the diffracting plane, λ is the wavelength of the incident radiation and d is the interplanar spacing of the diffracting planes. (Further information on Bragg’s Law is found in the TLP on X-ray diffraction).
In reciprocal space this can be expressed in the form
k' – k = g
where k is the wave vector of the incident wave of magnitude 2π/λ, k' is the wave vector of the diffracted wave, also of magnitude 2π/λ, and g is a reciprocal lattice vector of magnitude 2π/d:
This can be shown graphically using the Ewald sphere construction:
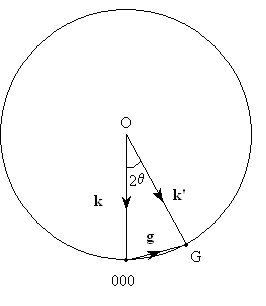
Here 000 is the origin of the reciprocal lattice and O is the centre of the sphere of radius \(\left| {\bf{k}} \right|{\rm{ }}\). If the angle subtended at O between 000 and G on the above diagram is 2θ, simple geometry shows that
\[\sin \theta = {{\left| {\bf{g}} \right|} \over {2\left| {\bf{k}} \right|}} = {{{{2\pi } \over {{d_{hkl}}}}} \over {2.{{2\pi } \over \lambda }}} = {\lambda \over {2{d_{hkl}}}}\]
which can be rearranged into the more familiar form
\[\lambda = 2{d_{hkl}}\sin \theta \]
i.e., the Bragg equation.
The equation
k' – k = g
can be rearranged in the form
k' = k + g
Hence
k'.k' = (k + g).(k + g) = k.k + g.g + 2k.g
Since k'.k' = k.k because diffraction is an elastic scattering event, it follows that
g.g + 2k.g = 0
To construct the Bragg Plane, it is convenient to replace k by -k in this equation so that both k and g begin at the origin, 000, of the reciprocal lattice. Hence, the equation can be written in the form
\[{\bf{k}}.\left( {{1 \over 2}{\bf{g}}} \right) = \left( {{1 \over 2}{\bf{g}}} \right).\left( {{1 \over 2}{\bf{g}}} \right)\]
Constructing the plane normal to g at the midpoint, \({1 \over 2}{\bf{g}}\), then means that any vector k drawn from the origin, 000, to a position on this plane satisfies the Bragg diffraction condition: