Close packing and packing efficiency
In many cases the atoms of a crystal pack together as tightly as possible. Approximating atoms as hard spheres they will achieve this by forming a close-packed structure. This is the case for most metallic structures.

The main ideas of close packing are demonstrated in the animation below
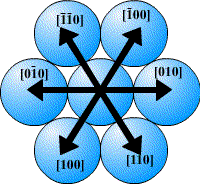
In a close-packed structure the close packed directions are the directions in which atoms are touching. For a hcp structure the close packed directions are [100], [010] and [110] and their negatives. Directions that are related by symmetry are represented using the notation <UVW>. The close packed directions for hcp are then <100>.
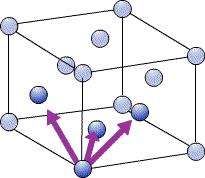
The close packed directions for ccp, which has a fcc unit cell, are along the diagonals of each face, [110], [101], [011]… etc. The set of directions that are related to these by symmetry are the <110> set.
Packing Efficiency
The packing efficiency of a crystal structure tells us how much of the available space is being occupied by atoms. It is usually represented by a percentage or volume fraction.
The packing efficiency is given by the following equation:
$${{\left( {number\,of\,atoms\;per\;cell} \right)*\left( {volume\;of\,one\,atom} \right)} \over {volume\;of\;unit\;cell}}\,$$
The steps usually taken are:
- Calculate the volume of the unit cell
- Count how many atoms there are per unit cell
- Calculate the volume of a single atom and multiply by the number of atoms in the unit cell
- Divide this result by the volume of the unit cell
The steps are straightforward. The main source of difficulty is expressing the volume of the unit cell in terms of the radii of the atoms (or vice versa). Knowing the close-packed directions makes this step easier for us. The animation below demonstrates how to calculate the packing efficiency of hcp, ccp and bcc structures.
Note: If you know the motif, an easy way to find the number of atoms per unit cell is to multiply the number of atoms in the motif by the number of lattice points in the unit cell.

