Diffraction and Imaging
AimsBefore you startIntroductionDiffraction patterns 1Diffraction patterns 2Two-dimensional diffractionImage formationInformation obtained from diffraction patternApplications of the theory of optical diffraction and imagingSummaryQuestionsGoing furtherTLP creditsTLP contentsShow all contentViewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext
Fraunhofer diffraction
Joseph von Fraunhofer (1787-1826)
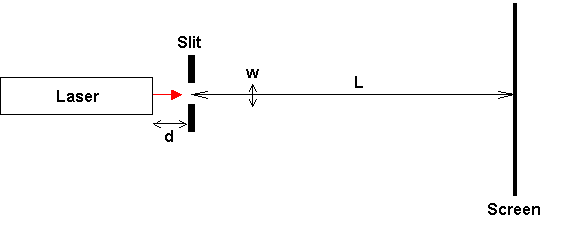
Fraunhofer diffraction occurs when the distances from the object to the source and the object to the image are so great that the incoming and outgoing waves are effectively planar. It is named after Joseph von Fraunhofer, who studied diffraction, and even built the first diffraction grating. The condition is given by
$${1 \over 2}\left( {{1 \over d} + {1 \over L}} \right){w^2} \ll \lambda $$
where d is the distance from the source to mask, L is the distance from mask to image, w is the width of the slit and λ is the wavelength of the radiation. If the condition is not met, then curvature of the waves is involved and the resulting effect is known as Fresnel diffraction.
