NonCommercial-ShareAlike 4.0 International
https://creativecommons.org/licenses/by-nc-sa/4.0/
Simulation of the Kirkendall Effect
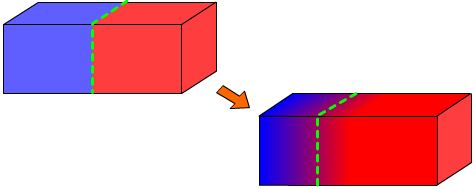
We will demonstrate the Kirkendall effect by simply modelling diffusion in two dimensions. In theory the Kirkendall effect should emerge from this model.

We start with two different coloured sets of points representing the two different materials. The white points represent vacancies and at every step each vacancy will swap places with a random adjacent atom.
Vacancies are created and destroyed at the edge of the material, representing vacancies entering and leaving. This simulation ignores vacancy creation and destruction within the bulk of the material.
source
concn
source
concn
Red
Vacancy
• Press the Start button to begin the simulation
• The Median line positions itself such that the number of diffused atoms on either side of the line is equal
• Pressing the Pause button will update the diffusion statistics. The statistics indicate how many blue atoms have crossed the Midpoint and how many red atoms have crossed the Midpoint. They also show many vacancies are present
• Change the vacancy creation rates using the sliders
When running the simulation for larger materials, it takes too long for the atoms to diffuse to a significant degree.
The following images are taken from a simulation which was left to run for 111,000 steps. Each frame shows a difference of 1000 steps.


The bottom image is a chart that shows the number of
blue atoms, red atoms and vacancies per column
From the simulation two pages back, one should have noticed that
the Median line moved to the left as time passed. This is the
Kirkendall effect.
We can also look at the pre-simulated data to check if the
Kirkendall effect emerges.
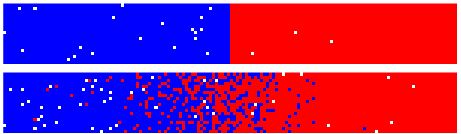
It is not very clear looking at the simulation pictures
so we will look at the graph pictures instead
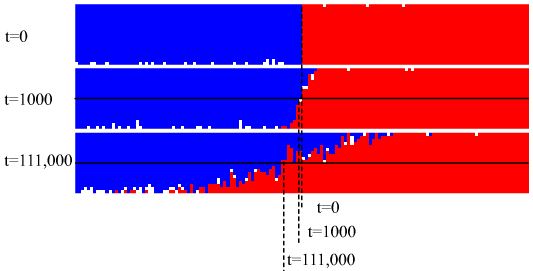
As we can see, the point of equal concentration moves
to left as time passes. This simulation, therefore, also
shows the Kirkendall effect