Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Diffusion Derivation of Fick's first law
Diffusion AimsBefore you startIntroductionDiffusion mechanismsRandom walkFick's first lawFick's second lawInterdiffusionMicrostructural effectsTemperature EffectsApplications of DiffusionSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Derivation of Fick's first law

Concentration gradient of impurity atoms across the crystal

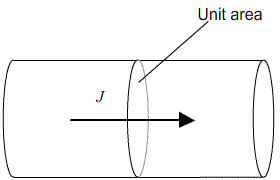
Fick’s first law relates this concentration gradient to the flux, J, of atoms within the crystal (that is, the number of atoms passing through unit area in unit time)

Number of atoms passing through unit area in unit time

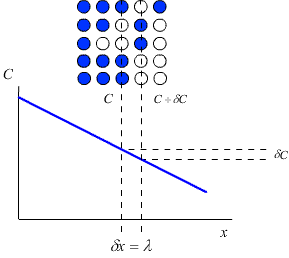
Each plane within a crystal will contain Cλ atoms per unit area.

This means that for an increment of distance (δx) of λ, the corresponding increment of concentration (δC) is given by:

\[\partial C = \lambda \left\{ {\frac{{\partial C}}{{\partial x}}} \right\}\]

For a three-dimensional crystal, an atom can move in one of six directions. If the jump frequency is ν, the fluxes of atoms from left to right and from right to left are given by:

\[{J_{L \to R}} = \frac{1}{6}\nu C\lambda \] \[{J_{R \to L}} = \frac{1}{6}\nu (C + \partial C)\lambda \]

Therfore the net flux, J, is given by:

\[ J = {J_{L \to R}} - {J_{R \to L}}\] \[J = - \frac{1}{6}\nu \partial C\lambda \] \[J = - \frac{1}{6}\nu \left\{ {\frac{{\partial C}}{{\partial x}}} \right\}{\lambda ^2}\] \[J \equiv - D\left\{ {\frac{{\partial C}}{{\partial x}}} \right\}\]

This is Fick’s first law: D is the diffusivity of the diffusing species.

PreviousNext