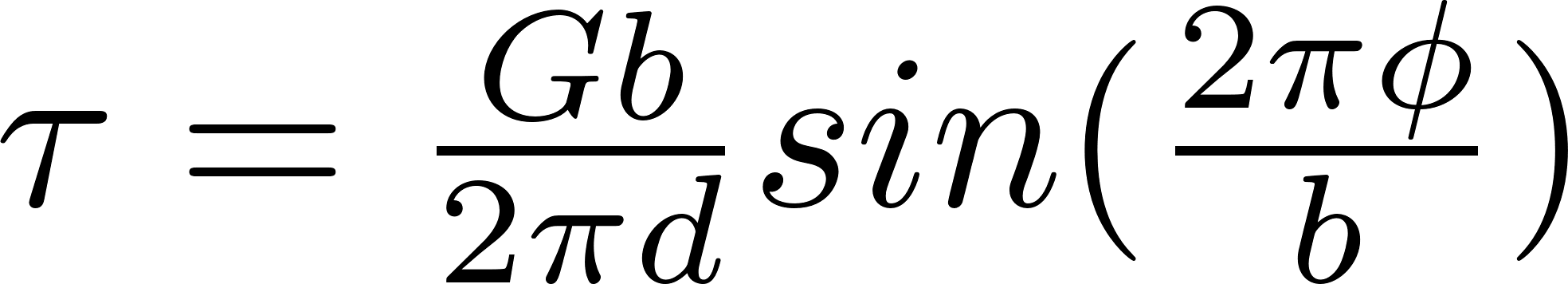NonCommercial-ShareAlike 4.0 International
https://creativecommons.org/licenses/by-nc-sa/4.0/
We know that the misfit energy of a dislocation is equal to αGb2 where α is about 1/2 and b is the Burgers vector, derived using continuum linear elasticity.
In continuum, the properties are the same everywhere, so there would be no energy change from place to place. Therefore we need to think atomistically.
There are two components of the misfit energy. These are:
Misfit energy due to in-plane strains
We assume the bonds are linear elastic. The change
in potential for a single lines of atoms of unit length is given by:
Hover over the components of the equation for an explanation
Hence this expression can also be written as:
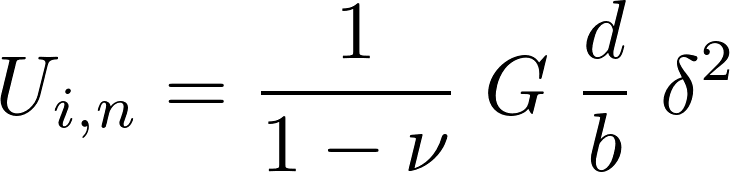
Volume = b · d · l
(l is the unit length of the line of atoms)
Strain
This is equivalent to δ/b where δ is the displacement of the bond length from its equilibrium value.Misfit energy due to misalignment between atoms across the slip plane
The Frenkel estimate of stress due to a misalignment φ
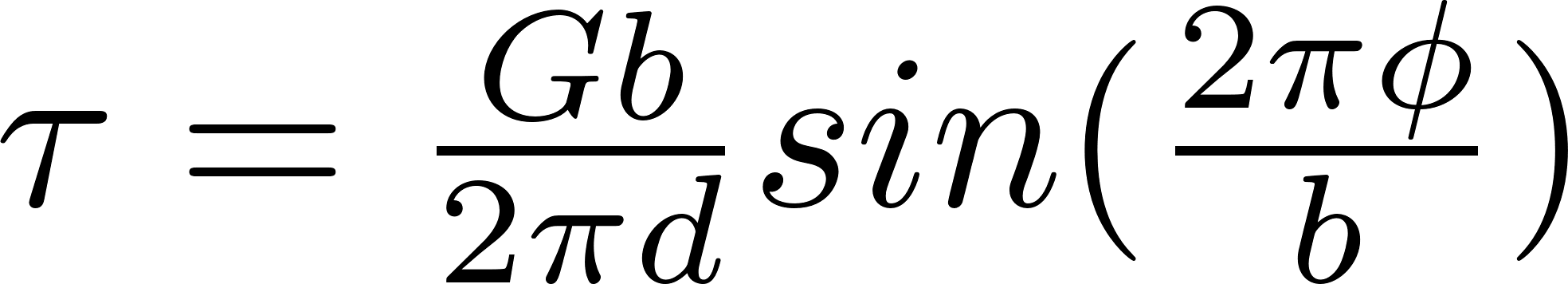
We integrate this with respect to φ and multiply by b to give the misalignment of a given pair of atom lines each of unit length:
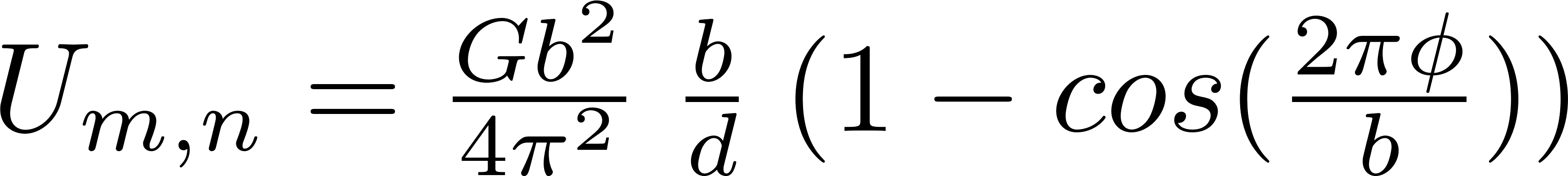
However this does not include the next-nearest neighbour term! Click next...
Now we need to sum together all the components of the misfit energy due to both the in-plane strain and the misalignment
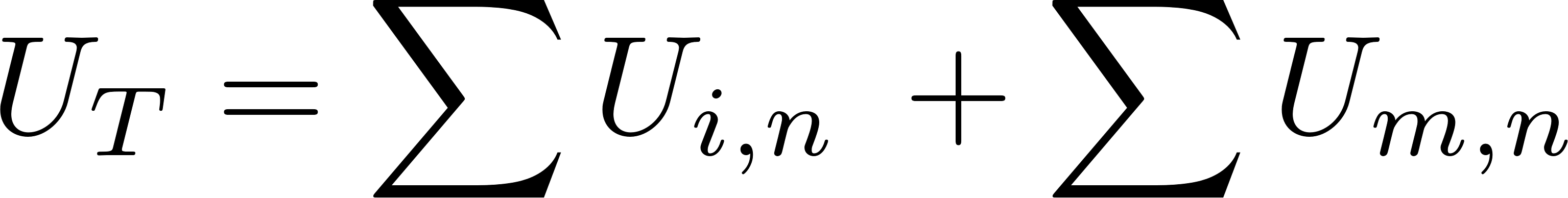
ε x = (1/E) (σx - ν(σy + σz )
ε y = (1/E) (σy - ν(σx + σz )
ε z = (1/E) (σz - ν(σx + σy )
In plane strain (in the x-y plane) means that that: εz = 0
Therefore if we set the third equation equal to zero, we get σz = ν ( σx + σy )
Subbing this into the expressions for ε x and ε y gives
ε x = (1/E) ( σx(1 - ν2) - σy( ν (1 + ν) ) )
ε y = (1/E) ( σy(1 - ν2) - σx( ν (1 + ν) ) )
Then since we are only applying stress in the x direction, εy = 0, so ε x = (1/E) ( σx(1 - ν2) )
We can therefore write the effective Young's modulus as Eeff = E / (1 - ν2 )
We need to consider the misalignment between nearest neighbour φ and next-nearest neighbour φ'.
Hence we obtain the following expression, where we have taken the average potential between the two atoms φ and φ'
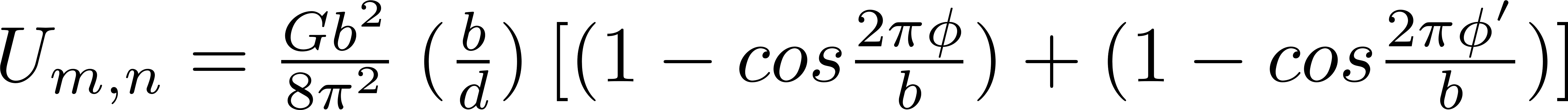
We consider how τ, the shear stress, varies with φ, the misalignment.
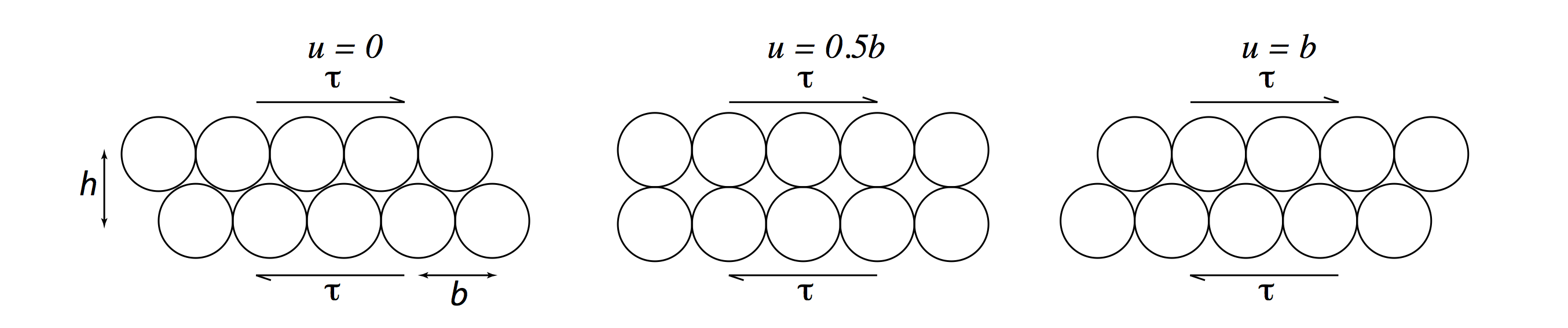
It is clearly a periodic dependence so we can write: 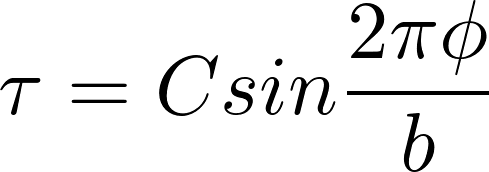
By writing the shear strain as γ = φ / d , and using the relation τ = Gb , we can find C.
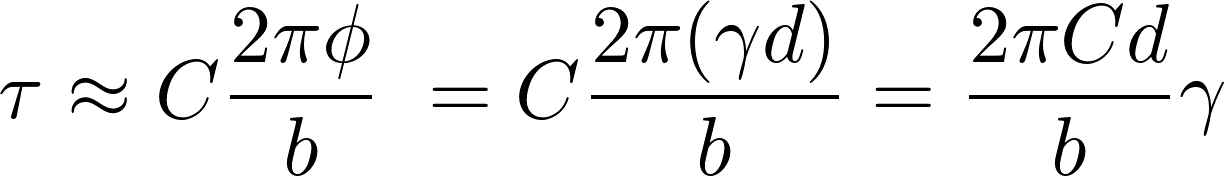
This means that 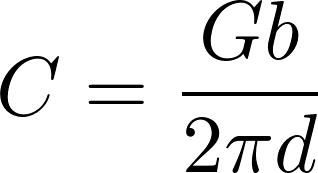 and so
and so