Ellingham Diagrams (all content)

Note: DoITPoMS Teaching and Learning Packages are intended to be used interactively at a computer! This print-friendly version of the TLP is provided for convenience, but does not display all the content of the TLP. For example, any video clips and answers to questions are missing. The formatting (page breaks, etc) of the printed version is unpredictable and highly dependent on your browser.

Contents

Aims

On completion of this Teaching and Learning Package you should:

• Be aware of the structure, origin and use of the Ellingham Diagram;
• Be able to use the interactive diagram included to find thermodynamic data quickly and effectively including:
  • ΔG, k, p_O2 for a standard and non-standard reactions across a range of temperatures;
  • Relative stabilities of elements with respect to oxidation etc or conversely that of oxides, sulphides etc;

Before you start

There are no special prerequisites for this TLP.

Introduction

The Ellingham Diagram, originally constructed for oxides, is a tool to find a variety of thermodynamic data quickly, without the need for repetitive calculation.

The diagram is essentially a graph representing the thermodynamic driving force for a particular reaction to occur, across a range of temperatures. With the data for several reactions plotted on the same graph, the relative stabilities of different elements with respect to, for example, their oxides, can be seen. It is also possible to compare the relative driving force for an element for oxidation or sulphidation in an environment containing both oxygen and sulphur as reactants.

Thermodynamics

Here we shall go through the basic thermodynamics that lies behind use of the Ellingham diagram. First, we will establish the link between the thermodynamics of a reaction and its chemistry.

The Gibbs free energy, G, of a system can be described as the energy in the system available to do work. It is one of the most useful state functions in thermodynamics as it considers only variables contained within the system, at constant temperature and pressure.

It is defined as:

\(G = H - TS\)        (1)

Here, T is the temperature of the system and S is the entropy, or disorder, of the system. H is the enthalpy of the system, defined as;

\(H = U + {\rm{p}}v\)        (2)

Where U is the internal energy, p is the pressure and v is the volume.

To see how the free energy changes when the system is changed by a small amount, we can differentiate the above functions:

\({\rm{d}}G = {\rm{d}}H - T{\rm{d}}S - S{\rm{d}}T\)        (3)

and;

\({\rm{d}}H = {\rm{d}}U + {\rm{pd}}v + v{\rm{dp}}\)        (4)

From the first law,

\({\rm{d}}U = {\rm{d}}q' - {\rm{d}}w\)        (5)

and from the second law,

\({\rm{d}}S = \) \({{{\rm{d}}q'} \over T} \) ,        (6)

we see that,

\(\displaylines{ {\rm{d}}G = {\rm{d}}q' - {\rm{d}}w + {\rm{pd}}v + v{\rm{dp}} - T{\rm{d}}S - S{\rm{d}}T \cr = - {\rm{d}}w + {\rm{pd}}v + v{\rm{dp}} - S{\rm{d}}T \cr = v{\rm{dp}} - S{\rm{d}}T \cr} \)        (7)

since work, \({\rm{d}}w = {\rm{pd}}v\)

The above equation shows that if the temperature and pressure are kept constant, we see that the free energy does not change. This means that the Gibbs free energy of a system is unique at each temperature and pressure.

At a constant temperature dT = 0 and so

\({\rm{d}}G = v{\rm{dp}}\)        (8)

We can find G for the system by integration. To do this we need the system’s equation of state, to give a relationship between v and p.

We will consider an ideal gas. For one mole of an ideal gas the equation of state is;

\(v = \) \({{RT} \over {\rm{p}}}\) ,       (9)

so (8) becomes

\({\rm{d}}G =\) \( RT{{{\rm{dp}}} \over {\rm{p}}}\)         (10)

Integrating:

\(G = RT\ln \left( {\rm{p}} \right) + const.\)        (11)

This we can express as

\(G = G^\circ + RT\ln \)\(\left( {{{\rm{p}} \over {{\rm{p}}^\circ }}} \right)\)        (12)

We define G° to be the standard free energy at the standard pressure, p°. These standard values are nothing more than lower integration constants, but using them is very useful, as we shall see. They are a consequence of the fact that one can only describe energy changes absolutely – there is no absolute energy scale, so the energy value we give to a system is arbitrary.

Chemical Reactions

We will now see why studying the free energy of a system is useful in determining its behaviour.

The free energy change, ΔG, of a chemical reaction is the difference in free energy between the products of the reaction and the reactants. If the free energy of the products is less than the free energy of the reactants there will be a driving force for the reaction to occur.

For the reaction

$${\rm{A}} + {\rm{B}} \to {\rm{C}}$$,

the free energy change,

\(\Delta G{\rm{ = }}{{\rm{G}}_{\rm{C}}}{\rm{ - }}{{\rm{G}}_{\rm{A}}}{\rm{ - }}{{\rm{G}}_{\rm{B}}}{\rm{ }}\)                (13)

\( = \Delta G^\circ + RT\ln \) \(\left( {{{{{{p_c}} \over {{p^0}_c}}} \over {{{{p_A}{p_B}} \over {{p^0}_A{p^0}_B}}}}} \right) \) (14) 
$$ = \Delta G^\circ + RT\ln \left( {{{{p_c}} \over {{p_A}{p_B}}}} \right)$$

if the standard states \(p_A^ \circ = p_B^ \circ = p_C^ \circ = {\rm{1bar}}\). We see that the free energy change of a reaction is determined by the relative quantities of reactants and products.

The Equilibrium Constant

A chemical reaction will occur if the total free energy of the products is less than the total free energy of the reactants. (ie. The free energy change for the reaction is negative.) If the system containing the reactants and products is closed (if there is no input of reactants, for example), the concentration of reactants will decrease and the concentration of products will increase as the reaction proceeds. This will alter the state of the system and therefore alter the free energy change for the reaction (see equation 14, above).

The reaction will continue if the free energy change remains negative. Hence, the system proceeds down a free energy gradient with respect to composition and this gradient provides the driving force for the reaction to proceed. The system alters the quantities of reactants and products in response to the driving force until a minimum in free energy is reached and the gradient is zero. This is a point of equilibrium.

At equilibrium the free energy change for the reaction is equal to zero:

$$\displaylines{ \Delta G = \Delta G^\circ + RT\ln \left( {{{{p_C}} \over {{p_A}{p_B}}}} \right) \cr = 0 \cr} $$
Therefore

$$\displaylines{ \Delta G^\circ = - RT\ln {\left( {{{{p_C}} \over {{p_A}{p_B}}}} \right)_{equilibrium}} \cr = - RT\ln {K_P}. \cr}\;\;\;\;(15) $$     

For the composition at equilibrium, the quotient is equal to G_P - the equilibrium constant for the reaction at constant pressure. We see that the equilibrium composition of the system is defined by the standard free energy change, ΔG°. Equation 15 provides a link between the thermodynamics of a reaction and its chemistry. ΔG° for a reaction is hence a very useful value to know.

The Ellingham diagram

The Ellingham diagram plots¹ the standard free energy of a reaction as a function of temperature. Originally the values were plotted for oxidation and sulphidation reactions for a series of metals, relevant to the extraction of metals from their ores (extraction metallurgy). These reactions generally involve the reaction of a gaseous phase (the oxidising gas) with (almost) pure condensed phases (the metal and oxidised compounds).

By using the diagram the standard free energy change for any included reaction can be found at any temperature. Along with allowing you to calculate the equilibrium composition of the system, the data on the diagram is useful in other ways, as we shall see.

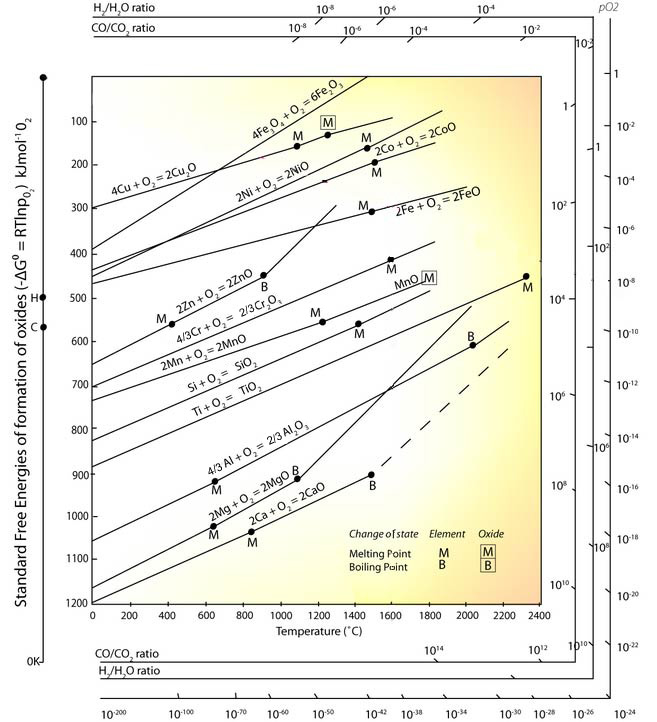
Note: Due to shortage of reliable experimental data, some of these lines are not plotted over the complete range of temperature.

¹ Ellingham H. J. T., J Soc Chem Ind (London) 63 125 (1944)

Applications

We shall consider the following reactions on the Ellingham diagram below: the oxidation of silver to form Ag₂O _(s); and the oxidation of cobalt to form CoO _(s) and Co₃O₄:

4Ag _(s) + O₂ = 2Ag₂O _(s);

2Co + O_{2 (g)} = 2CoO _(s)

3Co + 2O_{2 (g)} = Co₃O_{4 (s)}.

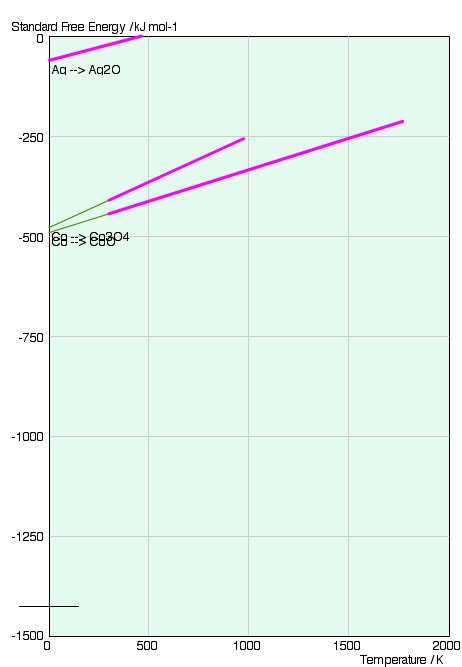
The graph consists of lines of

$$\Delta G^\circ = \Delta H^\circ - T\Delta S^\circ $$

Although ΔS and ΔH vary with temperature (see here to see why), the changes are so small as to be negligible, and so the lines are approximately straight. This means that they are of the form

$$y = mx + c$$

We can immediately see that the standard free energy change is greater (more negative) for the cobalt reaction relative to that of silver at all temperatures. This means that at all temperatures the equilibrium constant is larger for the cobalt reaction-the composition is further weighted towards the products of the reaction.

This is the reason that metals that appear higher up on the diagram are more stable than those metals that appear lower down, and are more likely to be found in their pure solid form. The gradient of the two lines is approximately the same.

We can see that the gradient of the lines is simply the standard entropy change for the reactions;

$${{\partial \Delta G^\circ } \over {\partial T}} = - \Delta S^\circ $$

This is evident from the reactions, which both involve the elimination of one mole of gas - a large decrease in entropy. This is the reason for the positive slope of the lines.

The reason for the change in slope is the change in phase of a component of the system, which alters the entropy change.

As the standard free energy change for both reactions is still negative (below 460K) the large decrease in entropy must be counteracted by a large enthalpy of reaction. This is indeed the case. The intercept of the lines with 0K gives the enthalpy of the reaction:

$${\left. {\Delta G^\circ } \right|_{0K}} = \Delta H^\circ $$

We can hence see that the relative stability of the oxide of cobalt compared with the oxide of silver is due to the much larger standard enthalpy of reaction.

Partial pressure of reacting gas

Using equations (15) we can see that the equilibrium constant is related to the partial pressures of reacting gases:

$${K_P} = {{{p_C}} \over {{p_A}{p_B}}}$$

for the reaction \({\rm{A}} + {\rm{B}} \to {\rm{C}}\). (Remember that these pressures must be related to a standard state.)

For a metal oxidation reaction ,

2M _(s) + O_{2 (g)} = 2MO _(s) ,

the equilibrium constant has the form

$${K_P} = {1 \over {p_{{O_2}}^{}}}$$

Click here for a more detailed discussion of the equilibrium constant.

We can therefore find the equilibrium partial pressure of oxygen at a particular temperature from the value of ΔG°:

$${\left. {{p_{{O_2}}}} \right|_{eq.,T}} = \exp {{\Delta G^\circ } \over {RT}}$$

The equilibrium partial pressure of oxygen is the pressure at which the driving force for the reaction is zero. From equation 14 we see that if the partial pressure of oxygen is greater than this value, the free energy change for the reaction is negative and there is a driving force for the reaction to take place. Metal will be oxidised, and the partial pressure of oxygen will drop until it reaches equilibrium. This is effect described by Le Chatelier’s principle.

If the partial pressure of oxygen is below the equilibrium value, oxidation is avoided. (In fact, the metal oxide will disassociate to form metal plus oxygen gas-this is because there is a driving force for the reaction to proceed backward. For this reason the equilibrium partial pressure is often known as the dissociation pressure.)

Reading p_O2 from the Ellingham diagram

In to avoid calculating the equilibrium partial pressure for each value of ΔG°, Richardson² added a nomographic scale to the Ellingham diagram. The equilibrium partial pressure is found as follows:

A line is drawn from the origin of the graph (T = 0, ΔG = 0) through the point on the Ellingham line of interest, at the required temperature. The equilibrium partial pressure is read off at the point where the drawn line crosses the nomographic scale.

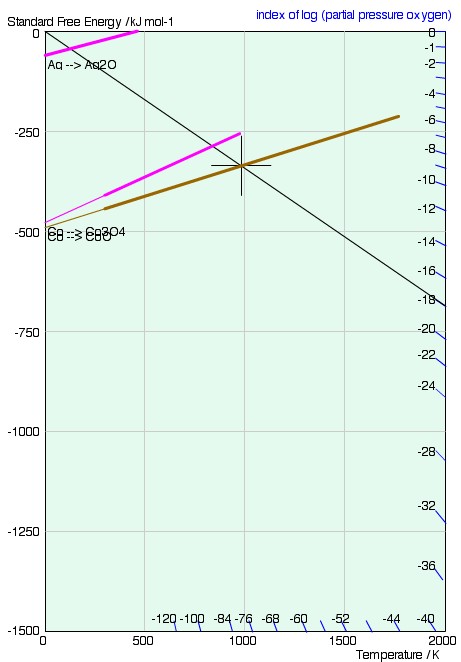
The scale is simply derived by considering the change in free energy of one mole of ideal gas, from p = 1 atm to p = P. We know that \(\Delta G^\circ = RT\ln {{\rm{p}}_{{{\rm{O}}_{\rm{2}}}}}\)and using equation 12 (\(G = G^\circ + RT\ln\)\( \left( {{{\rm{p}} \over {{\rm{p}}^\circ }}} \right)\)) we find that this is equal to the difference in free energy of a mole of gas at 1 atm and a mole of gas at P atm:

$$\Delta G = RT\ln {\rm{P}}$$

ie. a line from the origin with gradient RlnP. A series of lines for different values of the partial pressure, P, is shown below.

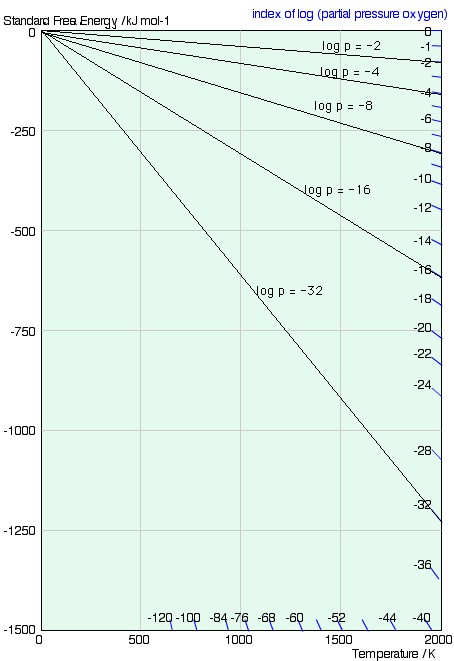
² F.D. Richardson and J.H.E. Jeffes, "The Thermodynamics of Substances of Interest in Iron and Steel Making from 0°C to 2400°C: I-Oxides," J. Iron and Steel Inst. (1948), 160 261.

Other gas mixtures

The oxygen required to cause oxidation in the gas phase need not to come from oxygen gas. Consider the following reaction:

2CO _(g) + O_{2 (g)} = 2CO_{2 (g)}

For this reaction,

$${K_{{{CO} \over {C{O_2}}}}} = {{p_{C{O_2}}^2} \over {p_{CO}^2.{p_{{O_2}}}}}$$

or $${p_{{O_2}}} = {{p_{C{O_2}}^2} \over {p_{C{O_{}}}^2.{K_{{{CO} \over {C{O_2}}}}}}}$$

and hence

$$\displaylines{ \ln {1 \over {{p_{{O_2}}}}} = \ln {K_{{{CO} \over {C{O_2}}}}} + 2\ln {{p_{C{O_{}}}^{}} \over {p_{C{O_2}}^{}}} \cr = {{ - \Delta G} \over {RT}} \cr} $$

We see that p_O2 is equivalent to a ratio: $${{p_{C{O_2}}^{}} \over {p_{CO}^{}}}$$ .

Another nomographic scale may be added to the diagram, with a new origin, C where the CO/CO₂ line crosses the y-axis.

Similarly for the reaction 2H₂ + O₂ = 2H₂O; p_O2 is equivalent to $${{p_{{H_2}O}^{}} \over {p_{{H_2}}^{}}}$$ Adding a further nomographic scale to the diagram, we see that the equilibrium pressure ratios of CO and CO₂ or H₂ and H₂O for a given oxidation of metal, or reduction of an oxide, can be deduced at a given temperature from the diagram.

Reducing agents

A major application of the Ellingham diagram is the determination of the conditions required to reduce metal compounds, such as oxides or sulphides, to obtain pure metal. This is often the basis of extraction metallurgy, the extraction of metals from their ores. It is also very important in the recycling of metals. See the Ellingham Diagram section of Recycling of Metals TLP for more information.

A chemical is a reducing agent with respect to a particular metal when the free energy change for its oxidation is more negative than the free energy change of oxidation of the pure metal. This means that when the reducing agent is placed in a closed system containing the metal ore there is a driving force for the dissociation of metal and oxidiser (ie. oxygen or sulphur gas, for example).

Consider the two oxidation reactions below, whose lines on the Ellingham diagram cross each other:

2A + O₂ = 2AO       (a)

and

B + O₂ = BO₂.        (b)

As we can see, the y-intercept, ΔH°_(a) , of the first reaction is greater than the y-intercept of the second reaction, ΔH°_(b) . Since the lines cross, the gradient of the second line, ΔS°_(b) , is greater than that of the first.

At the point that the lines cross the standard free energy changes for two reactions are equal. This means that a closed system containing the metals A and B will be at equilibrium. This can be shown by considering the reaction below, obtained by subtracting reaction (a) from reaction (b):

B + 2AO = 2A + BO₂

At T = T_E , ΔG for this reaction is zero, and no reaction occurs. However above this temperature A is reduced by B, and below it B is reduced by A.

Drawing a line from the origin through the point at which the lines cross and extending it to the nomographic scale for oxygen pressure gives the partial pressure of oxygen at equilibrium.

Consider the reaction

3C + 2Fe₂O₃ = 3CO₂ + 4Fe

ΔG is only negative for this reaction above T=1020K. Hence, steel furnaces operate above 1020K.

Other atmospheres

An Ellingham diagram may be drawn for other systems where the gaseous phase is not oxygen but another gas such as chlorine. This is useful for industrial processes where the environment is a mixture of gases.

Non-standard states

In calculating the various thermodynamic quantities above we have assumed that the condensed metal phase is pure.

In many cases, however, the metal is in the form of an alloy – perhaps in solid solution with other metals. In this case the metal is not in its standard state, and its ability to participate in a reaction – its activity – is reduced. This affects the free energy change for the reaction (which is no longer the standard free energy change) and means that the pressure of reacting gas required for equilibrium between the metal in solution and the pure product is changed.

These values can be found by substituting the modified activity of the metal into the expression for the equilibrium constant and ΔG:

$$\eqalign{ & K = {1 \over {{p_{B({\rm{M in standard state)}}}}}} = {1 \over {{a_M}p_{B({\rm{M in alloy)}}}^{}}} \cr & \Rightarrow {p_{B({\rm{M in alloy)}}}} = {{{p_{B({\rm{M in standard state)}}}}} \over {{a_M}}};{\rm{ and}} \cr} $$

$$\Delta G = \Delta G^\circ - RT\ln {a_M}$$

where a_M is the activity of the metal in the alloy.

Graphically, a decrease in activity has the effect of rotating the Ellingham line for the reaction anti-clockwise around its intersection with T = 0.

Summary

In the preceding pages we have seen that the standard free energy change for a reaction is a very useful quantity to know, in that its value affects the equilibrium constant and gives composition of the system.

We have also seen that the Ellingham diagram is a convenient way of displaying the standard free energy change of many reactions at different temperatures. We have also seen how to read the value of p_O2 from the Ellingham diagram.

Finally, we have seen how the Ellingham diagram is used in extraction metallurgy to find the conditions needed for reduction of metal ores.

The interactive Ellingham diagram

The interactive Ellingham diagram included within this TLP is a teaching and learning tool, which you can use to obtain a variety of useful thermodynamic information pertaining to a wide range of reactions.

Click on this link to launch the interactive Ellingham diagram in a new window.

Click to on this link to open the diagram’s User Guide in a new window.

Please note that the diagram is for educational purposes only, and the accuracy of the data contained within it is not guaranteed.

Interactive Ellingham diagram user guide

Questions

Quick questions

You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

1. The Ellingham diagram shows values of which thermodynamic quantity as a function of temperature?

   	a	Standard electrode voltage;
   	b	Standard free energy change of reaction;
   	c	Partial pressure of gas;
   	d	Enthalpy change of reaction.

2. For a closed system at equilibrium at a temperature T, which of the following statements are true?

   1. ΔG = 0;
   2. ΔG° = 0;
   3. ΔH = TΔS;
   4. ΔS = 0.

3. Why are the slopes of many of the lines on the Ellingham diagram almost identical?

   	a	Most reactions involve the elimination of one mole of gas, so there is a similar standard enthalpy change of reaction.
   	b	Most reactions involve the elimination of one mole of gas, so there is a similar standard entropy change of reaction.
   	c	The activity of most of the metals is the same.
   	d	The partial pressure of the reacting gas is the same for all reactions.

4. What thermodynamic quantity does the intercept at T=0 K for any standard free energy vs T line signify?

   	a	The approximate value of the standard entropy change;
   	b	The approximate value of the standard enthalpy change;
   	c	The equilibrium constant for the oxidation reaction;
   	d	Heat capacity of the oxide.

5. What is the decomposition temperature (to the nearest 50 K) for Ag₂O? (This question should be completed with the help of the interactive Ellingham diagram included with this TLP).

   	a	460 K
   	b	500 K
   	c	540 K
   	d	620 K

6. What is the decomposition temperature (to the nearest 50 K) for PdO? (This question should be completed with the help of the interactive Ellingham diagram included with this TLP).

   	a	1050 K
   	b	1100 K
   	c	1150 K
   	d	1200 K

7. Which of the following elements can be used to produce Cr from Cr₂O₃ at 1200K? (This question should be completed with the help of the interactive Ellingham diagram included with this TLP).

   1. Mg
   2. Fe
   3. Co
   4. Al

8. Explain, using the Ellingham diagram, how a mixture of Cl₂/O₂ gas may be used to separate Zn from Fe in a galvanised scrap. (This question should be completed with the help of the interactive Ellingham diagram included with this TLP).

Going further

Books

• D.R. Gaskell, "Introduction to the Thermodynamics of Materials" (Taylor and Francis, 1995) Third ed.
  Provides a good treatment of the Ellingham diagrams pp.347-395.
• E.T. Turkdogan, "Physical Chemistry of High Temperature Technology" by (Academic Press, 1980)
  Main data source for the interactive diagram and deals with the physical chemistry of iron and steelmaking in ch.9.

Academic consultant: R. Vasant Kumar (University of Cambridge)
Content development: James Chivall and David Brook
Photography and video: Brian Barber
Web development: Lianne Sallows

This DoITPoMS TLP was funded by the UK Centre for Materials Education and the Department of Materials Science and Metallurgy, University of Cambridge.

Additional support for the development of this TLP came from the Worshipful Company of Armourers and Brasiers'