Why are some materials magnetic?
It was discovered by Oersted in 1820 that a magnetic compass needle was deflected when placed near to an electric current; this was a breakthrough in the understanding of magnetism that later led to Ampère observing that the magnetic field of a solenoid being identical to that of a magnet.
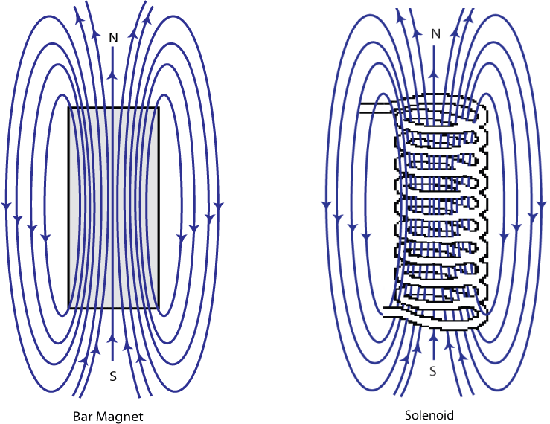
Figure F. Schematic showing the shape of the magnetic field around a bar magnet and a solenoid are identical.
Ampère then hypothesised that all magnetic effects were due to current loops and that the magnetic effects in materials must be due to “molecular currents”, attributed to the movement of electrons. However, the currents predicted by this model were unfeasibly large and a second origin of magnetism was required. This second magnetic mechanism was spin, postulated by Dirac in 1928, after he solved the fully relativistic quantum mechanical equations governing the electron.
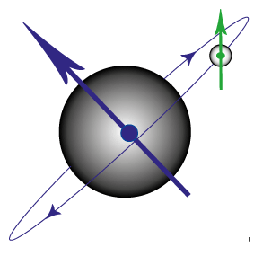
Figure G. Diagram to show the magnetic moment produced by an electron orbiting the nucleus and that produced by the spin of the electron.
The spin of an electron is hard to visualise, but has the properties of a small magnetic moment pointing either “up” or “down”. Within an atom, electrons are arranged in orbitals, with a maximum of two electrons with opposite spin occupying each orbital (due to the Pauli Exclusion Principle). The orbitals are further grouped into shells. In all atoms except for hydrogen there is more than one electron and these electrons can interact with each other as well as with the nucleus, leading to “coupling”.
Coupling
As outlined above, the total magnetic moment of a free atom has two contributions from each electron:
- The angular momentum as the electron orbits the nucleus (strictly, the momentum of the nucleus relative to the orbiting electron). This is effectively Ampère’s molecular current and is known as the orbital contribution.
- The ‘spin’ of the electron itself
In an atom with a single electron, there are just two magnetic fields produced which can interact (see above figure). The magnetic field from the electron’s spin interacts with the magnetic field from its movement around the nucleus, leading to so-called spin-orbit coupling.
In an atom with more than one electron, the total magnetic moment of the atom will depend on the spin-orbit (intra-electron), spin-spin (inter-electron) and orbit-orbit (also inter-electron) coupling. The spin-orbit coupling is weak for light atoms and generally can be ignored in calculating the total angular momentum.
The total magnetic moment can be determined by simple vector addition of the fields.
Important results of this coupling are as follows. When working out the moment on an atom, only incomplete electron shells (groups of orbitals) contribute. Furthermore, electrons arrange themselves in shells in such a way as to maximise total spin. Putting these two results together, we see that once a shell is more than half full, spins begin to pair up within orbitals and the available magnetic moment decreases. This underlies the existence of magnetic order in elements in the middle of the 3d series and the middle of the 4f series.

