Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Granular Materials Mapping of Mohr-Coulomb theory onto (q,p') space
Granular Materials AimsBefore you startIntroductionTerzaghi's effective stress principleGround settlement and centrifuge modelling experimentsAngle of reposePrinciple of normalityYielding of disturbed saturated soils in triaxial stress testsOriginal Cam-Clay modelLiquefactionWet sand drying underfootSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Mapping of Mohr-Coulomb theory onto (q,p') space

Mohr-Coulomb theory is a theory in (τ, σ) space, or, if there is pore water pressure u, (τ,σ') space where σ' = σ – u.

When considering how to map Mohr-Coulomb theory onto (q, p') space, we can first plot the yield surface in (τ, σ') space in the way conventionally plotted in soil mechanics, with compressive stresses positive:

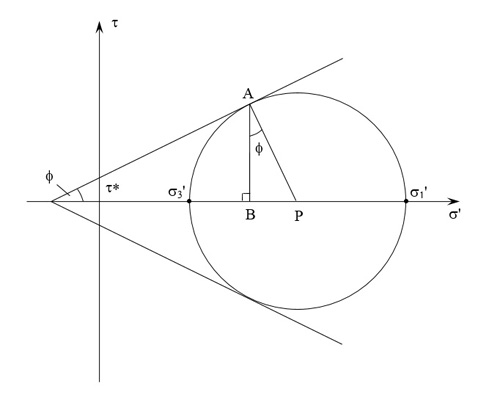
Failure occurs when the plane subjected to a normal stress \({\sigma'_{n}}\) represented on the horizontal axis by the point B is further subjected to a shear stress of magnitude BA. If we represent BA by τ, then

\[ {\tau} = \tau ^* + {\sigma'_{n}}\tan \phi       (1) \]

In this failure criterion \({\sigma'_{1}}\)and \({\sigma'_{3}}\) are the maximum and minimum compressive principal stresses. The third compressive principal stress, \({\sigma'_{2}}\) , is between these two and is not specified. If we choose the third compressive principal stress to be the arithemetic mean of \({\sigma'_{1}}\) and \({\sigma'_{3}}\), i.e.,

\[{\sigma '_2} = \frac{{{{\sigma '}_1} + {{\sigma '}_3}}}{2}\]

then the centre of Mohr’s circle is simply p'. Furthermore, if we identify q with the largest possible deviatoric stress, then q = \({\sigma'_{1}}\) \({-}\) \({\sigma'_{3}}\), i.e., the diameter of the Mohr’s circle.

With these links, simple geometry shows that

\(\frac{{p' - {{\sigma '}_n}}}{{q/2}} = \sin \phi \) and \(\frac{\tau }{{q/2}} = \cos \phi \)

Hence, we can transform equation (1) into the equation

\[\frac{q}{2}\cos \phi = \tau^* + (p' - \frac{q}{2}\sin \phi )\tan \phi \]

which simplifies to the equation

\[q = 2\tau^ *\cos \phi + 2p'\sin \phi \]

i.e., an equation of the form

\[q = {q_0} + mp'\]

PreviousNext