Derivation of yield ellipse aspect ratio
For plane stress, let the principal stresses be 
and 
, with 
.
The yield surfaces for the Tresca yield criterion and the von Mises yield criterion are shown below.
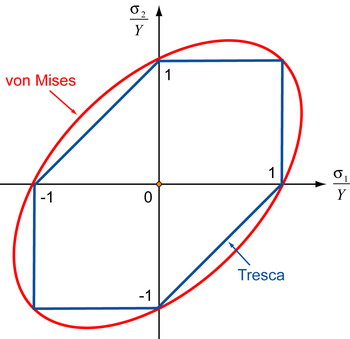
The Tresca yield surface is an irregular hexagon and the von Mises yield surface is an ellipse. The ratio of the length of the major and minor axes of this ellipse is 
.
In the quadrant where 
and 
, the Tresca yield surface is a square.
To see this, first suppose 
for example. Since 
, yield occurs on the Tresca criterion when
i.e., for 
because 
. When 
, yield occurs at 
. Similarly, for 
in this quadrant, yield occurs when 
.
The shape of the Tresca yield surface in the quadrant where 
and 
is a straight line because the third principal stress 
will be the intermediate principal stress. Hence in this quadrant the yield criterion becomes
whence the straight line linking 
to 
in the diagram. The shape of the Tresca yield surface in the remaining two quadrants follows similarly.
For plane stress the von Mises yield criterion becomes
which for 
becomes
i.e.,
Thus the yield surface for plane stress passes through 
, 
, 
, 
, 
, and 
. It also passes through the points
as can be seen by direct substitution in the yield condition for 
.
The directions
are orthogonal and their magnitudes define the length of the major and minor axes of this ellipse.
Hence, the ratio of the length of the major and minor axes of this ellipse is 
.
back
© 2004-2012 University of Cambridge.