Yield criteria for non-metals
When ceramics deform plastically (usually only at temperatures very close to their melting point, if at all), they often obey the von Mises or Tresca criterion.
However, other materials such as polymers and geological materials (rocks and soils) display yield criteria that are not independent of hydrostatic pressure.
Empirically, it is found that as a hydrostatic pressure is increased, the yield stress increases, and so we do not expect a yield criterion based solely on the deviatoric component of stress to be valid.
The first attempt to produce a yield criterion incorporating the effect or pressure was derived by Coulomb.
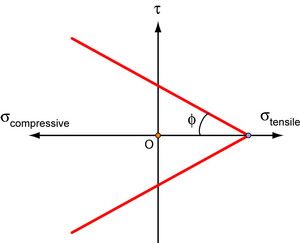
The Coulomb criterion
Failure occurs when the shear stress, τ, on any plane reaches a critical value, τc, which varies linearly with the stress normal to that plane.
\[{\tau _c} = {\tau ^*} - {\sigma _n}\tan \phi \]
where 
is the positive normal stress on the plane of failure (so that on this convention, a compressive stress or pressure is a negative quantity), 
is a material parameter and 
is the angle of shearing resistance. (Note: 
is not a ‘coefficient of friction’ although often referred to as such).
Failure locus for soil
For soils, tanφ ≈ 0.5 - 0.6 typically. So as a soil is compressed, τc increases.
If the principal components of stress are σ1,
σ2,
σ3 for a particular
stress state at some point within a soil mass, we can draw three Mohr’s
circles with diameters specified by σ1 > σ3
; σ2 > σ3
; σ1 > σ2.
For failure, we require only one of these to touch the failure locus, e.g.
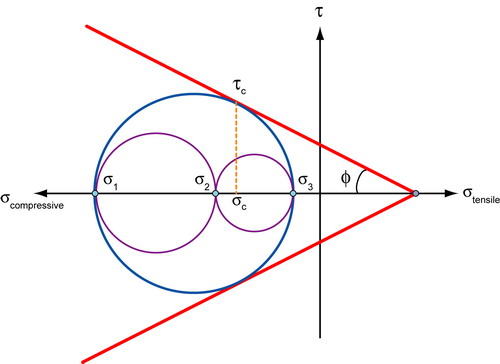
Here, failure is determined by \(\left| {{\sigma _1} - {\sigma _3}} \right|\),
not by σ2.
This is therefore a variant or modification of the Tresca criterion.
Example Problem 2: Yield criteria for non-metals
A better model for polymers is to assume that the shear stress k at which failure occurs is a function of hydrostatic stress or pressure, e.g.
$$k = {k_0} + \mu P$$
where \(P = - \)\(\frac{1}{3}\)\(\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right) = - {\sigma _H}\) = hydrostatic pressure and k0 is the value of shear yield stress at zero hydrostatic pressure.
If we do this, we obtain pressure-modified criteria, which work well for polymers. For example, the pressure-modified von Mises criterion has a circular sectional cone with its axis along σ1 = σ2 = σ3:
$${\left( {{\sigma _1} - {\sigma _2}} \right)^2} + {\left( {{\sigma _2} - {\sigma _3}} \right)^2} + {\left( {{\sigma _3} - {\sigma _1}} \right)^2} = 2{Y^2} = 6{k^2} = 6\left( {{k_o} + \mu P} \right)$$
The pressure-modified Tresca criterion has a hexagonal pyramid with axis along σ1 = σ2 = σ3:
$$\left( {{\sigma _1} - {\sigma _3}} \right) = Y = 2k = 2\left( {{k_0} + \mu P} \right)$$
These modified criteria work well for polymers.