Questions

Deeper questions

The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

1. A specimen of sheet steel is tested in unequal biaxial tension, and Lüders bands form at 60° to one of the tensile axes. Show that the ratio between the two principal stresses in the plane of the sheet is 1:5.

   If the greater of these two principal stresses is 500 MPa and the steel obeys von Mises' yield criterion, show that the yield stress in uniaxial tension is 458 MPa.

2. Use a work formula approach to estimate the minimum pressure required to extrude aluminium curtain rail of I-section, 12 mm high with 6 mm wide flanges, all 1.6 mm thick, from 25 mm diameter bar stock.

   [The mean uniaxial yield stress for aluminium for heavy deformation at room temperature is 150 MPa. The minimum pressure, 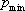, required is given by the formula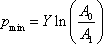

   

   where 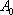 is the original cross-sectional area and  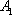is the cross-sectional area of the extruded I-section].

3. The diagram below shows a possible deformation pattern for the direct plane-strain extrusion of a metal slab, initially 40 mm thick, through a symmetrical 45° tapering die, with an extrusion ratio of 2.The diagram shows half the deformation pattern and the angles BCD and CBD are both 45°. The distance AB is 15 mm. The width of the slab is 100 mm and its yield stress in pure shear is 150 MPa.

   

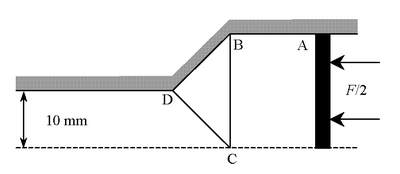
   Calculate an upper bound to the extrusion force F acting on the slab if the extrusion process is frictionless.