Molecular weight
This section should strictly be called “Polymer molecular mass”, but in polymer science it is more common to refer to molecular weight than molecular mass, so this convention will be continued here.
The molecular weight of a synthetic polymer does not have a single value, since different chains will have different lengths and different numbers of side branches. There will therefore be a distribution of molecular weights, so it is common to calculate the average molecular weight of the polymer. However, there are several different ways to define the average molecular weight, the two most common being the number average molecular weight and the weight average molecular weight. Other averages exist, such as the viscosity average molecular weight, but they will not be discussed here.
When studying a polymer, the most relevant average depends on the property being investigated: for example, some properties may be more affected by molecules with high molecular weight than those with low molecular weight, so the weight average is chosen since it highlights the presence of molecules with high molecular weight.
The average molecular weight of a polymer sample can be determined using a variety of techniques, such as gel permeation chromatography, light-scattering measurements and viscosity measurements, and the type of average that is yielded depends on the technique.
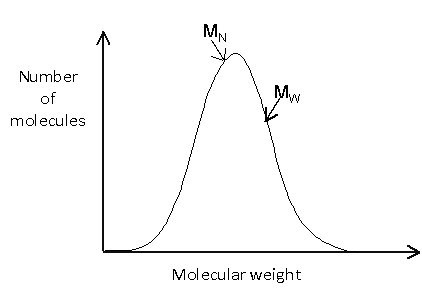
Number average molecular weight, N
The number average molecular weight is defined as the total weight of polymer divided by the total number of molecules.
Total weight \( = \sum\limits_{i = 1}^\infty {{N_i}{M_i}} \)
where Ni is the number of molecules with weight Mi
Total number \( = \sum\limits_{i = 1}^\infty {{N_i}} \)
The number average molecular weight is therefore given by:
$$\overline {{M_N}} = {{\sum\limits_{i = 1}^\infty {{N_i}{M_i}} } \over {\sum\limits_{i = 1}^\infty {{N_i}} }}$$
This can also be written as:
$$\overline {{M_N}} = \sum\limits_{i = 1}^\infty {{x_i}{M_i}} $$
where xi is the number fraction (or mole fraction) of polymer with molecular weight Mi.
Weight average molecular weight, w
The weight average molecular weight depends not only on the number of molecules present, but also on the weight of each molecule. To calculate this, Ni is replaced with NiMi.
$$\overline {{M_W}} = {{\sum\limits_{i = 1}^\infty {{N_i}M_i^2} } \over {\sum\limits_{i = 1}^\infty {{N_i}{M_i}} }}$$
This can also be written as:
$$\overline {{M_W}} = \sum\limits_{i = 1}^\infty {{w_i}{M_i}} $$
where wi is the weight fraction of polymer with molecular weight Mi.
The weight average molecular weight is therefore weighted according to weight fractions.
Polydispersity Index
The polydispersity index is defined as the ratio of the weight average molecular weight to the number average molecular weight, and it gives a measure of the distribution of the molecular weight within a sample. It has a value greater than or equal to one: it is equal to one only if all the molecules have the same weight (i.e. if it is monodisperse), and the further away it is, the larger the spread of molecular weights.
Polydispersity index \( = {\raise0.7ex\hbox{${\overline {{M_W}} }$} \!\mathord{\left/
{\vphantom {{\overline {{M_W}} } {\overline {{M_N}} }}}\right.\kern-0em}
\!\lower0.7ex\hbox{${\overline {{M_N}} }$}}\)
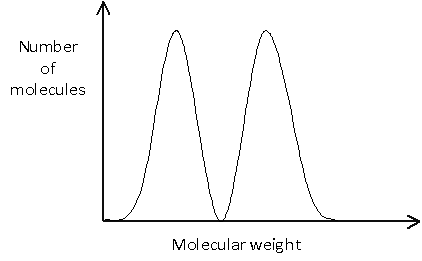
Molecular weight distributions
The molecular weight distribution can be shown graphically by plotting the number of molecules against the molecular weight. It is worth noting that these plots are sometimes shown with molecular weight decreasing along the x-axis.
The distribution may be relatively simple, such as:
Or it may be more complicated, such as:
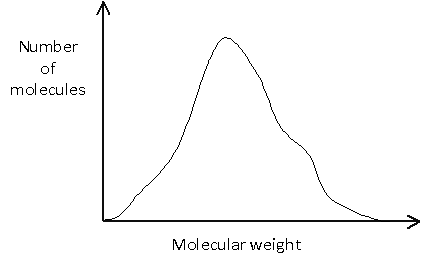
In many cases, it is important to know not only the average molecular weight, but also the distribution of molecular weights. This is illustrated in the example below, in which no molecules would actually have a weight equal to the number average molecular weight, since this would lie between the two peaks.