Reciprocal Space (all content)

Note: DoITPoMS Teaching and Learning Packages are intended to be used interactively at a computer! This print-friendly version of the TLP is provided for convenience, but does not display all the content of the TLP. For example, any video clips and answers to questions are missing. The formatting (page breaks, etc) of the printed version is unpredictable and highly dependent on your browser.

Aims
Before you start
Introduction
Reciprocal space
Mathematical representation of reciprocal lattice
Ewald sphere
Applications of reciprocal space
Summary
Questions
Going further

Aims

On completion of this TLP you should:

understand what a reciprocal lattice is
understand the construction of a reciprocal lattice from a known real lattice
understand the importance of reciprocal space in planning experiments and interpreting diffraction data

Before you start

To understand the application to diffraction you will find it helpful to complete the TLPs on Crystallography and X-ray techniques first.

To understand the construction and results of the reciprocal lattice you will need to first understand conventional unit cells.

Introduction

The concept of reciprocally has been introduced in the Diffraction and Imaging TLP, and in the X-ray Diffraction TLP within the Bragg and Scherrer equations. This inverse scaling between real and reciprocal space is based on Fourier transforms.

Josiah Willard Gibbs first made the formalisation of reciprocal lattice vectors in 1881. The reciprocal vectors lie in “reciprocal space”, an imaginary space where planes of atoms are represented by reciprocal points, and all lengths are the inverse of their length in real space.

In 1913, P. P. Ewald demonstrated the use of the Ewald sphere together with the reciprocal lattice to understand diffraction. It geometrically represents the conditions in reciprocal space where the Bragg equation is satisfied.

Later in the TLP, we will formalise the relationship between the real lattice vectors and unit cell and the reciprocal lattice, show the construction of the Ewald sphere and demonstrate some if its uses.

Reciprocal space

The animation below shows the relationship between the real lattice and the reciprocal lattice. Note that this 2D representation omits the c* vector, but that it follows the same rules as a* and b*.

The key things to note are that:

The reciprocal lattice has reciprocal vectors a* and b*, separated by the angle γ*.
a* is perpendicular to the (100) planes, and equal in magnitude to the inverse of d₁₀₀.
Similarly, b* is perpendicular to the (010) planes and equal in magnitude to the inverse of d₀₁₀.
γ and γ* will sum to 180º.

Due to the linear relationship between planes (for example, d₂₀₀ = ½ d₁₀₀ ), a periodic lattice is generated. In general, the periodicity in the reciprocal lattice is given by

${\rho _{hkl}}^ *$ = $\frac{1}{{{d_{hkl}}}}$

In vector form, the general reciprocal lattice vector for the (h k l) plane is given by

${s_{hkl}}$ = $\frac{{{{\rm{n}}_{hkl}}}}{{{d_{hkl}}}}$

where n_hkl is the unit vector normal to the (h k l) planes.

This concept can be applied to crystals, to generate a reciprocal lattice of the crystal lattice. The units in reciprocal space are Å^-1 or nm^-1

Mathematical representation of reciprocal lattice

We want reciprocal lattice vectors such that the reciprocal vector is the inverse in magnitude of the real vector and is normal to the planes separating the original vector.

So,

$$\left| {{\bf{a}}*} \right| = {1 \over {{d_{100}}}} = {1 \over {\left| {\bf{a}} \right|\cos (\gamma - {\pi \over 2})}}$$ and $${{{\bf{a}}*} \over {\left| {{\bf{a}}*} \right|}} = {{{\bf{b}} \times {\bf{c}}} \over {\left| {{\bf{b}} \times {\bf{c}}} \right|}}$$

Therefore,

$${\bf{a}}* = {{{\bf{b}} \times {\bf{c}}} \over {{\bf{a}}.{\bf{b}} \times {\bf{c}}}}$$and similarly:

$${\bf{b}}* = {{{\bf{c}} \times {\bf{a}}} \over {{\bf{a}}.{\bf{b}} \times {\bf{c}}}}$$

$${\bf{c}}* = {{{\bf{a}} \times {\bf{b}}} \over {{\bf{a}}.{\bf{b}} \times {\bf{c}}}}$$

Fourier Analysis of Periodic Potential

The periodic potential of a lattice is given by:

$U({\rm{r}}) = \sum\limits_k {{U_k}} \exp (i2\pi {\rm{K}}.{\rm{r}})$, where U_k is the coefficient of the potential, and r is a real position vector
However only values of K are allowed which are reciprocal lattice vectors (S).

Proof:

$U({\rm{r}}) = \sum\limits_S {{U_S}} \exp (i2\pi {\rm{S}}{\rm{.r}})$
since U_(r) = U_(r + R), where R is a lattice vector,

$\sum\limits_S {{U_S}} \exp (i2\pi {\rm{S}}{\rm{.r}}) = \sum\limits_S {{U_S}} \exp (i2\pi {\rm{S}}.({\rm{R}} + {\rm{r}}))$

$\sum\limits_S {{U_S}} = \sum\limits_S {{U_S}} \exp (i2\pi {\rm{S}}.{\rm{R}})$

λ = exp( i 2 π S R )

S R = n, where n is an integer.

Only possible values are of the form:

G = ha* + kb* + lc* as GR = h + k + l and h, k, l are integers.

Note: This is strictly the crystallographer’s definition of reciprocal lattice vectors. In solid-state physics, the 2π factor is included as a scalar within S. The 2π factor may be omitted depending on the application.

Ewald sphere

Consider a circle of radius r, with points B and C lying on the circumference.

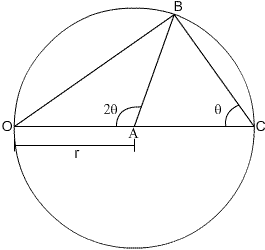
By using simple trigonometry,

\[\sin \theta = \frac{OB}{{2r}}\]

If this geometry is constructed in reciprocal space, then it has some important implications.

The radius can be set to 1/λ, where λ is the experimental wavelength.

If O is the (0 0 0) reciprocal lattice point, and B is a general point (h k l), then the distance OB is 1/d_hkl = S_hkl The reciprocal vector between the points, S, increases in magnitude with increasing 2θ,

Hence

$\sin \theta $ = $\frac{{\frac{1}{{{d_{hkl}}}}}}{{\frac{2}{\lambda }}}$

i.e.

λ = 2 d_hkl sin θ

The Ewald circle represents in reciprocal space all the possible points where planes (reflections) could satisfy the Bragg equation. In 3-dimensions an Ewald Sphere represents all the possibilities. For simplicity, it is often drawn as a circle in two dimensions.
The animation below shows how the Ewald circle is used in diffraction to determine the angles at which the Bragg equation is satisfied.

Now that you have seen the construction of the Ewald Sphere try finding some points yourself in this simulation:

In order to ‘measure’ a diffraction spot one has to position the detector (film or electronic) on the reciprocal lattice point.

Applications of reciprocal space

Ewald sphere and Reciprocal space for single crystal and oriented samples

Reciprocal space and the Ewald sphere have important implications for x-ray diffraction. Experiments are set up in real space. Some topics can be considered in either real or reciprocal space whilst others are simpler, or even only really work, in reciprocal space.

Ways to measure more reflections from a single crystal have been described in real space in the ‘X-ray diffraction’ TLP but are simpler to see in reciprocal space with the Ewald sphere construction.

To observe more reflections one can:

Rotate the reciprocal lattice (i.e. the sample) relative to the incoming x-ray beam.
Use a spread of wavelengths, i.e. ‘white radiation’, to give the Ewald sphere a substantial thickness instead of a thin surface. This is described in Laue photographs. An interesting application is on-line assessment of orientation in single crystals such as turbine blades.
Spread a reciprocal spot into a ring as used in powder diffraction.

Reciprocal Space Maps

This application for measuring the lattice parameters of a film as compared with those of the underlying substrate is shown in the following animation. Here it is much simpler to interpret the data in reciprocal space.

Systematic absences explained by the reciprocal lattice

For non-primitive lattices, systematic absences can occur in the reciprocal lattice and in the diffraction patterns. This is due to the construction of the lattices. Shown below is an example of how a larger unit cell is used instead of the primitive one. Because the shortest plane spacing along the lattice vectors becomes the longest repeating length along the reciprocal lattice vector direction, the magnitude of the reciprocal lattice vector is equal to its reciprocal length.

When the new reciprocal lattice is labelled with respect to the new reciprocal lattice vectors, the dashed spots are "absent".

These systematic absences are used to determine the lattice type, e.g. primitive, body or face-centred.

Indexing

Assigning indices to the diffraction spots and working out the unit cell is done in reciprocal space. This is described in the Indexing Electron Diffraction TLP.

Brillouin Zones

Brillouin Zones, an important tool in solid state physics, are also worked in reciprocal space.

Summary

Following completion of this TLP you should understand what a reciprocal lattice is, and how it is constructed. You should understand that the Ewald sphere is a geometric tool to find reflections and angles that satisfy the Bragg equation. Thus it is used to set up diffraction experiments and interpret the data. The package has also shown how reciprocal vectors are important in understanding periodic structures and diffraction, which have a reciprocal nature.

Questions

Quick questions

You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

What does a point in reciprocal space correspond to in real space?

a A lattice point

b A plane

c A lattice vector

d A unit cell

Open-ended questions

The following questions are not provided with answers, but intended to provide food for thought and points for further discussion with other students and teachers.

Use this Ewald Sphere to find the angle at which a (2 0 0) plane will satisfy the Bragg condition for this lattice and wavelength. (Assume that it is a primitive lattice):

Deeper questions

The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

What is the reciprocal lattice of a reciprocal lattice?
What is the reciprocal Bravais lattice of an FCC lattice?
What are the reciprocal lattice vectors of a lattice with 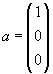, 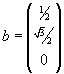and ?
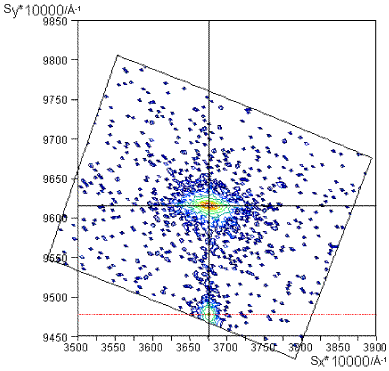
On the (105) maps below what are the in- and out-of-plane reciprocal space coordinates for the films? Try to convert them into real space cell parameters. (As shown previously c is out-of-plane and both films have hexagonal unit cells).
Al_xGa_(1-x)N
In_xGa_(1-x)N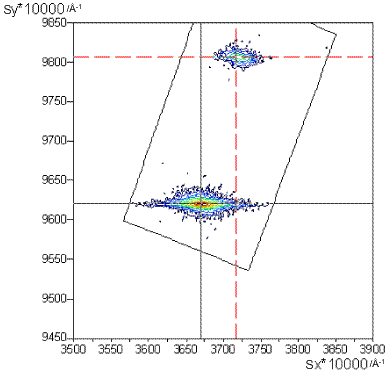

Going further

Books

Reciprocal space is described in most Crystallography books. For example:

C. Hammond, The Basics of Crystallography and Diffraction, 2nd edition, OUP, 2001
B. D. Cullity and S. R. Stock, Elements of X-ray Diffraction, 3rd edition, Prentice Hall, 2001
Eds F H Chung and D K Smith Industrial Applications of X-ray Diffraction 2000 has a chapter on history of Rolls Royce on-line Laue system

Websites

Indexing Electron Diffraction Patterns TLP uses reciprocal space to relate the diffraction pattern to real space.
Brillouin Zones, an important tool in solid state physics, are also worked in reciprocal space.

Academic consultant: Mary Vickers (University of Cambridge)
Content development: T D Skinner
Photography and video: Brian Barber and Carol Best
Web development: David Brook

This DoITPoMS TLP wass funded by the UK Centre for Materials Education and the Department of Materials Science and Metallurgy, University of Cambridge.

Additional support for the development of this TLP came from the Worshipful Company of Armourers and Brasiers'

Al_xGa_(1-x)N	In_xGa_(1-x)N