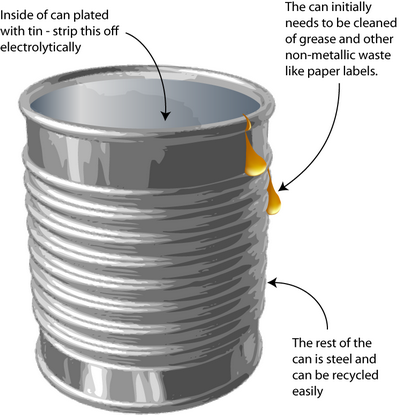
Tin can processing
Leaching and electrolysis of tin from steel cans
How do you remove the tin-plating from tin cans without dissolving the steel underneath? Solving this problem requires knowledge of the way in which metals corrode – an important concept in materials science.
The process is a little different today than explained here because the tin coating has been thinned (those who remember may have noticed the decreasing weight of ‘tin cans’ over the years).
The original method to remove tin from cans was stripping by electrolysis. Knowledge of electrochemistry is critical in the designing of this process. The tin plating must be removed without dissolving the steel underneath.
![]()
The reactions used
Pourbaix diagrams plot potential vs. pH. They describe the thermodynamic stability of metals that have oxidised components, as a function of the pH of the aqueous solution. Using these diagrams the most commonly used method for detinning steel has been designed.
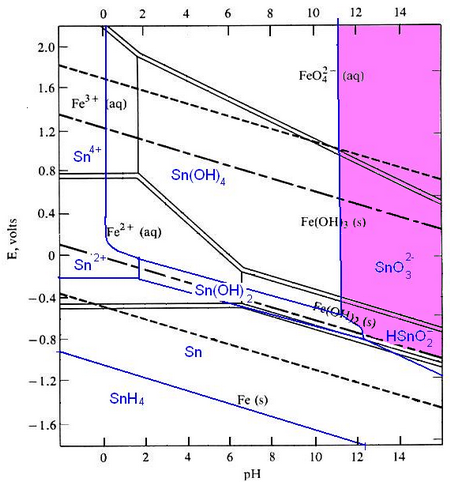
The Pourbaix diagrams for iron (black) and tin (blue) superimposed.
At a high pH (>12) – the purple region in the diagram - Sn can be stabilised in alkali solution as HSnO2– and as SnO32– in the presence of an oxidant. In this region of the diagram, iron is passivated and does not corrode. The oxidant helps this passivation to occur. In this way the tin can be removed from the surface of the can, while the steel is not harmed.
The electrochemical oxidation of the tin can be expressed as:
Sn(s) + 2H2O(l) = HSnO2– (aq) + 3H+ + 3e- (reaction 1)
Using the Nernst equation:
\[{E_{{\rm{rev}}}} = {E^0} + \frac{{RT}}{{6F}}\ln \alpha \]
We can write the electrode potential of this reaction as:
For a pH of 12 and [ HSnO2– ] of 10-2 mol, E = –0.79V. By convention this is expressed as the reduction potential, i.e. for the reverse of reaction (1). For the tin being dissolved, the potential is reverse in sign, i.e. E = +0.79V.
Under oxidising conditions, HSnO2– can be oxidised further to SnO32– :
HSnO2– + H2O = SnO32–(aq) + 3H+ + 2e- (reaction 2)
The Nernst potential for this is calculated:
\[E(V ) = 0.374 - 0.0886pH + 0.0295\log \left( {\frac{{[{\rm{SnO}}_3^{2 - }]}}{{[{\rm{HSnO}}_2^ - ]}}} \right)\]
For pH = 12 and [ SnO32– ] = [ HSnO2– ] = 10-2 mol, we find that E(v) = –0.69V.
This too is a reduction potential, i.e. for the reverse of Reaction 2. The potential for turning HSnO2– into SnO32– is +0.69V.
![]()
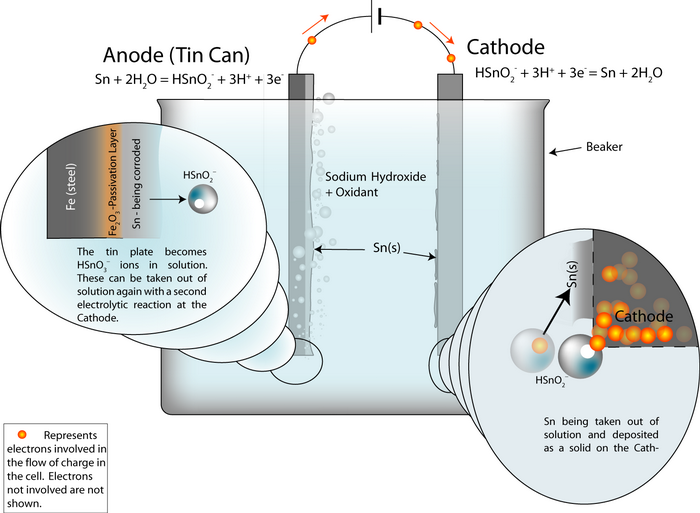
Setting up the process
An electrochemical detinning cell is arranged with the tin plated can as the anode. If the cell is arranged so that the reactions go backwards at a cathode plate, pure tin is deposited on the cathode.
Thus the overall cell reaction is Sn (anode)![]() Sn (cathode).
Sn (cathode).
The whole cell electrode potential is zero. The applied potential is not zero, because we need to put some energy in to overcome these energy barriers:
- Ohmic losses – the electrolyte, the connecting wires and the electrodes have electrical resistance.
- polarisation losses – the surfaces of the electrodes become charged and we need to supply the ions with enough energy to escape the charged layer.
In the same way as the aluminium cell, the whole cell electrode potential can be written as:
Ecell = Erev + ηA + ηC + (I · R)
where I is the current, R is the resistance of the components and ηA is the potential across the charged layer at the anode (and similar for the cathode).
![]()
The effect on the iron
At pH 12 and under oxidising conditions, the iron is passivated. Fe3O4 and/or Fe2O3 form an adherent, non-porous layer on the surface (a passivation layer). This slows down the rate of movement of Fe ions into solution and protects the iron from being dissolved. The presence of oxidising agents such as sodium nitrite makes the passivating layer form faster and more completely.
The passivation reaction producing Fe3O4 can be written as:
3Fe + 4H2O → Fe3O4 + 8H+ + 8e-
with a potential E0 = -0.085 - 0.0591 pH
Under oxidizing conditions, the passivating layer is Fe2O3:
2Fe3O4 + H2O → 3Fe2O3 + 2H+ + 2e-
with potential E0 =-0.221 - 0.0591 pH
At very high pH (>13), solutions can be corrosive to Fe, especially if they are free of oxidizing agents:
Fe + H2O → HFeO2– + 3H+ + 2e-
E0 = -0.2493 - 0.886 pH + 0.295 log [HFeO2-]
HFeO2– dissolves in the electrolyte and the steel can corrodes away.
The detinning process can be recreated in miniature in the laboratory:

