Diehls rule

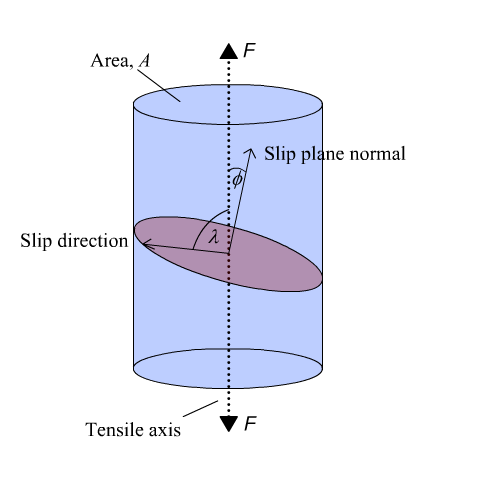
Single crystal slip and Diehl's rule

In single crystals, slip typically occurs on the closely-packed planes in well defined directions, i.e. in ccp metals, the slip system is {111}<110>. This slip can be examined using the stereogram, and can be predicted in the same way.

Firstly, we need to look at slip itself. Slip occurs on a slip plane, which has a normal at an angle of \( \phi \)° to the tensile axis. Slip occurs in the slip direction, at an angle of λ° to the tensile axis. The slip plane area is \( A / \cos\phi \), and the force is \( F \cos\) λ in the slip direction.

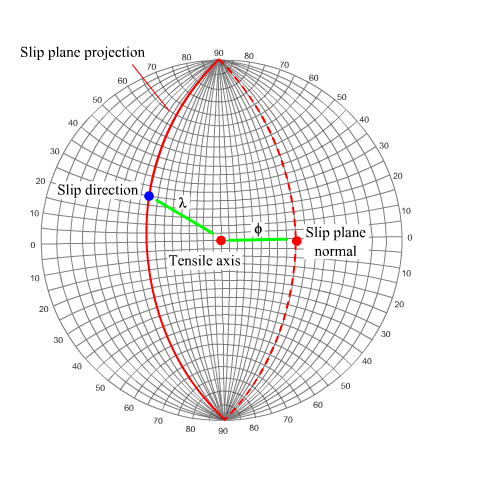
We can show this geometry on a stereogram as seen here:

The slip is caused by the tensile force, resolved into the slip direction, giving a resolved shear stress of:

\(\tau = \)\(\frac{F}{A}\) \(\cos \phi \cos \) λ

The factor \( \cos \phi \cos \) λ is called the Schmid factor. Slip occurs when \( \tau \) reaches a critical value on the slip plane(s) for which the Schmid factor is a maximum.

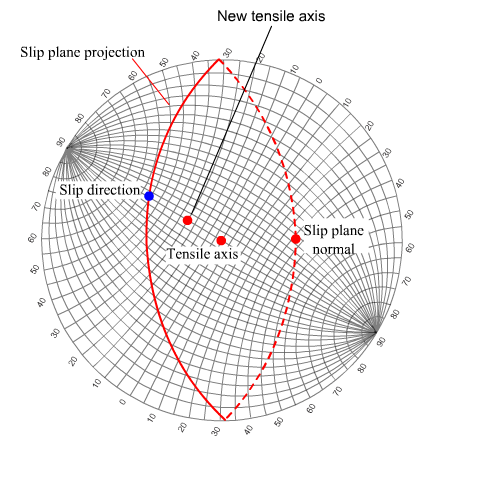
During slip, if the sample is not constrained, the ends move relative to each other.

Typically, in a tensile test the ends are constrained, meaning that the slip causes only internal motion. This results in rotation of the slip plane, so that the direction of slip rotates towards the tensile axis, or equivalently, the tensile axis rotates towards the slip direction.

Now, the slip direction is constrained to lie in the slip plane. Therefore, on the stereogram, this rotation is represented by the rotation of the tensile axis towards the slip direction, along the great circle joining the tensile axis to the slip direction.

The system on which slip occurs is the one with the highest Schmid factor. Diehl's rule can be used to find the slip system on which slip occurs, by using a stereographic method. This can be used to identify slip in ccp crystals: Slip system {111}<110> and bcc crystals: Slip system {110} <111>.

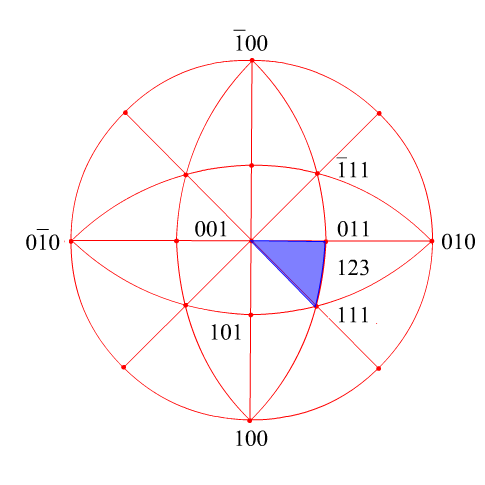
Use of Diehl's rule for ccp crystals

First, start with a standard cubic stereogram, showing all poles of the form {100}, {110} and {111}.
The great circles are
added to form 48
right-angled spherical triangles, 24 in the northern hemisphere and 24 in the southern hemisphere.

The next step is to identify the triangle containing the tensile axis. For example if the tensile axis is [123], it is located within the triangle constructed from 001, 011 and 111. It can be plotted using the techniques already covered in this TLP.
For cubic crystals, the
vector [123] is parallel
to the normal to the plane (123), and so all we need to do is identify the location of the normal to the (123) planes.

Reflection plane

To find the slip plane, take the {111} type pole in this triangle, and reflect it across the side of the triangle which it is opposite, i.e. reflecting
111 in the great
circle containing
001 and 011, giving the slip plane as (111).

Reflection plane

To find the slip direction, the <110> type pole in the triangle that contains the tensile axis is reflected in the great circle opposite to it.

This analysis allows us to quickly produce the slip system. We can now see that slip occurs on the (111) plane, and in the [101] direction.

Since we know that the tensile axis moves towards the slip direction, we can now predict the movement of the tensile axis.

It heads towards [101], i.e. towards the 101 pole on the stereogram, or equivalently, the location of the normal
to the (101) planes
since we are dealing
here with cubic crystals.

When it reaches the edge of the triangle, two slip systems are of equal Schmid factor. The slip system operating can change as the tensile axis moves.

At this point, the slip direction becomes the vector sum of the slip directions of the two slip systems, i.e. in this case,
the slip direction
now becomes [112].