NonCommercial-ShareAlike 4.0 International
https://creativecommons.org/licenses/by-nc-sa/4.0/
Basics of the Wulff net
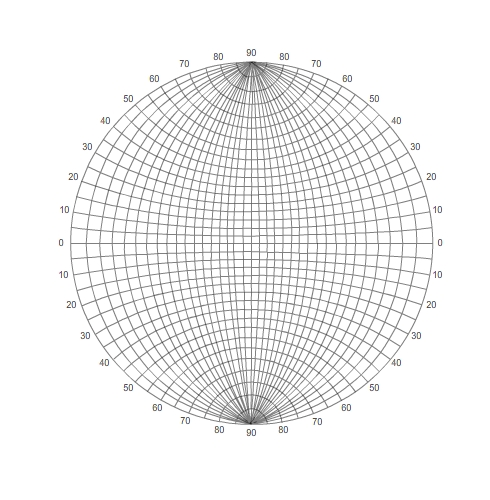
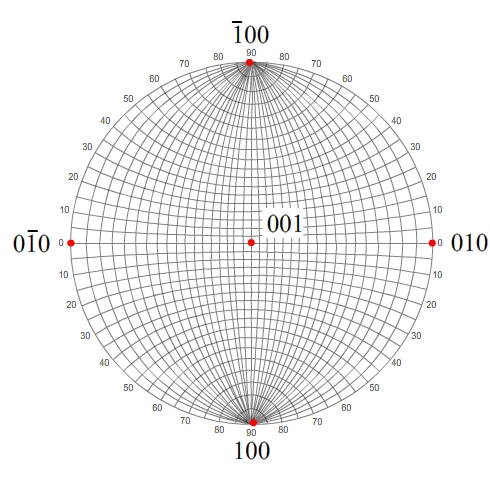
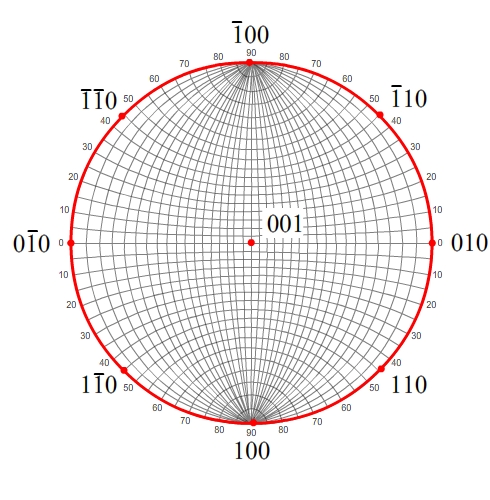
Typically, a Wulff net will be aligned down [001]. For crystal systems with orthogonal lattice vectors, such as cubic crystals, this means that the 001 pole is at the centre of the stereogram, with the 100 and 010 poles at 90° to 001 and to each other. It is conventional, but not a requirement, that the 010 pole is placed on the right-hand side of the stereogram as shown.
Primitive circle - [001] zone
100, 00, 010 and 00
all lie on the primitive circle, a special case of a great circle. The
primitive circle is the [001] zone, i.e. all planes whose normals lie
in this zone contain the [001] direction. This zone therefore contains
any pole of the form hk0.
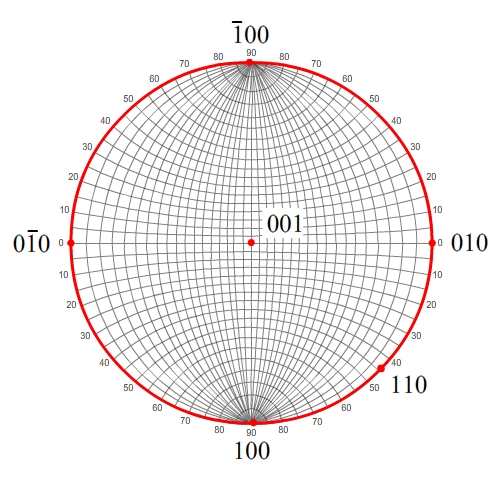
We can therefore plot any pole which is in the [001] zone, by measuring along the great circle until we reach its angular position relative to a reference, i.e. (110) is at 45° to (100), and so we measure 45° around the primitive circle to plot the pole of the plane (110).
It is then straightforward to plot other poles of the form hk0.
It is possible to plot poles which are of the more general
form hkl by utilising the zonal relationships between planes.
For example, (111) shares a zone with (110) and (001).
A zone on a Wulff net is represented by a great circle. All positions on this great circle represent the poles of planes lying within that zone. Therefore, to plot poles of planes within a zone, we need to rotate the Wulff net until a great circle lines up between the required poles.
We can then measure the required angular distance along that great circle to plot the next pole, i.e. (111) is 54.7° from (001), or 35.3° from (110).
This use of zones can be extended to allow you to draw every other possible pole. While it is possible to place a pole by using the (hk0) method, it is also possible to plot other poles by making use of other great circles. This can be demonstrated by plotting all planes of the form {111}
To plot poles which share the same zone, we need to align the poles on a great circle. 111 and 11 both lie in the same zone as each other, and the same zone as 010 and 00. So we can align the Wulff net as shown here, and then plot the next pole by measuring 70.5° along the great circles.
The remaining two poles can be plotted in the same manner.
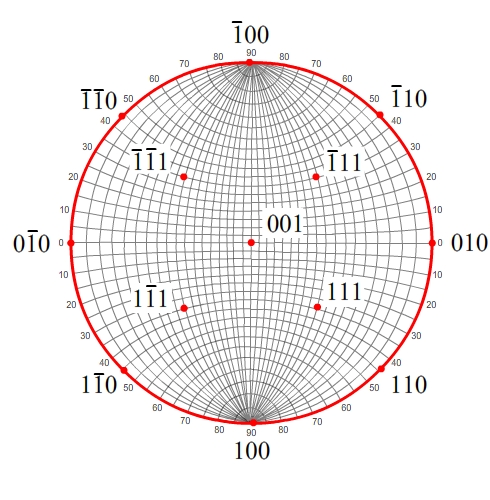
This is a rather simple construction to show how to make use of the Wulff net.
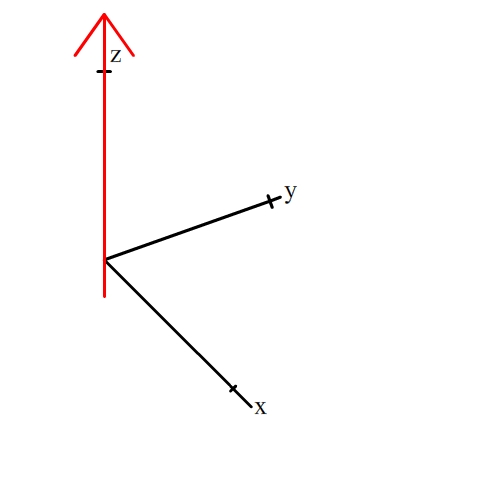
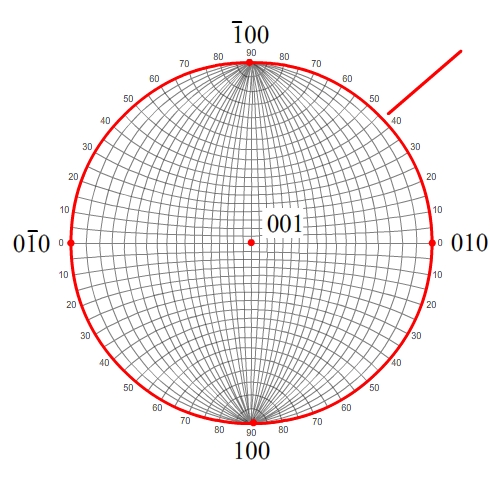
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
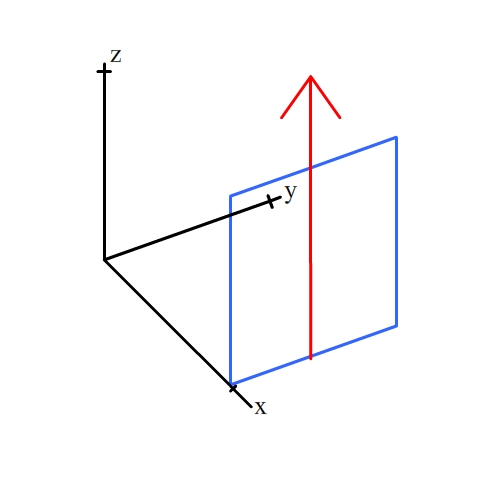
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
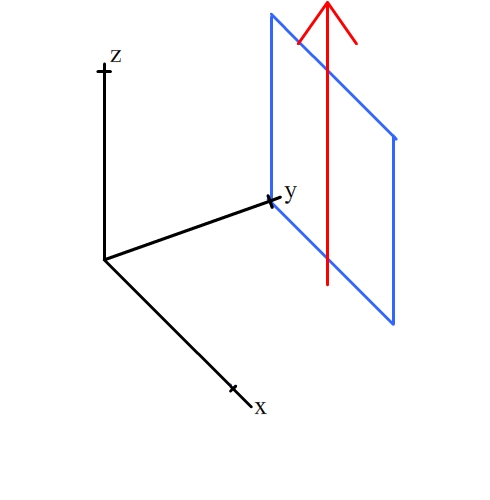
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
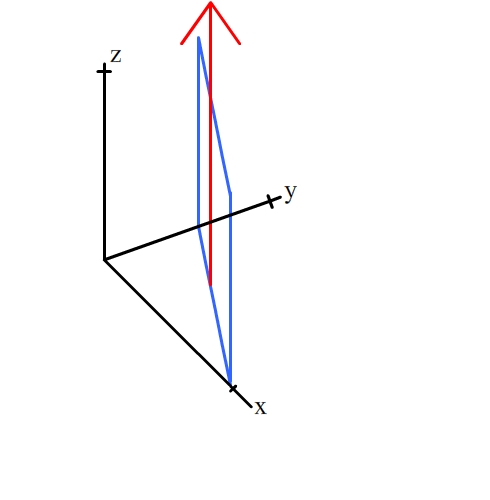
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
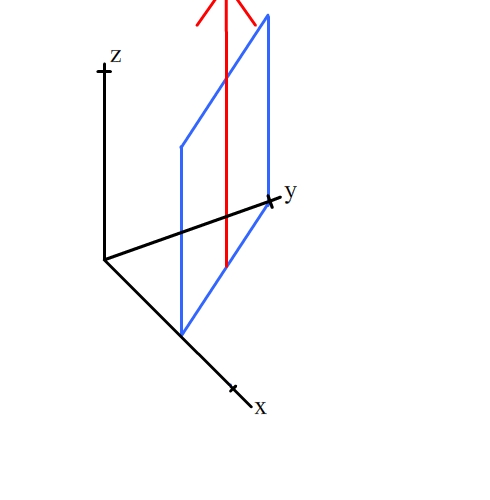
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
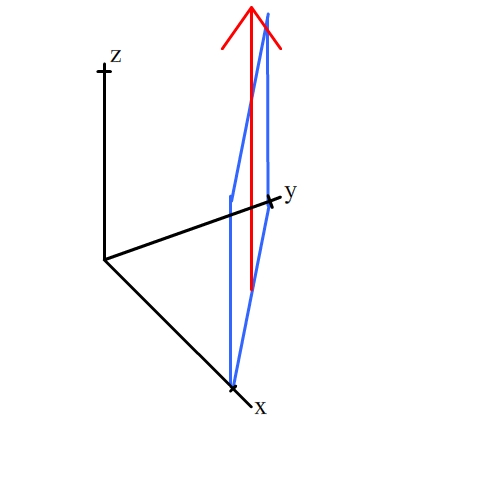
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
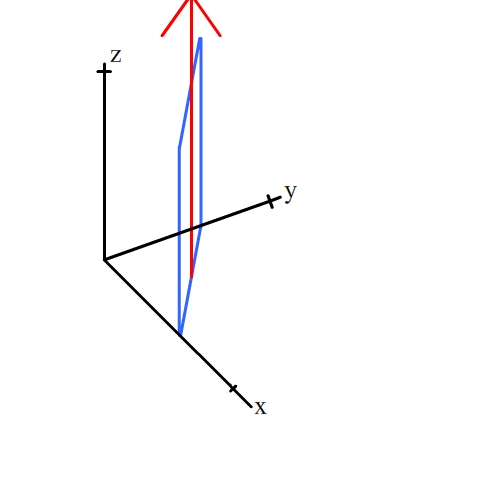
The [001] zone contains all planes of the form (hk0).
These planes contain the direction [001] (shown by the red arrow). For
an example, click on the planes below:
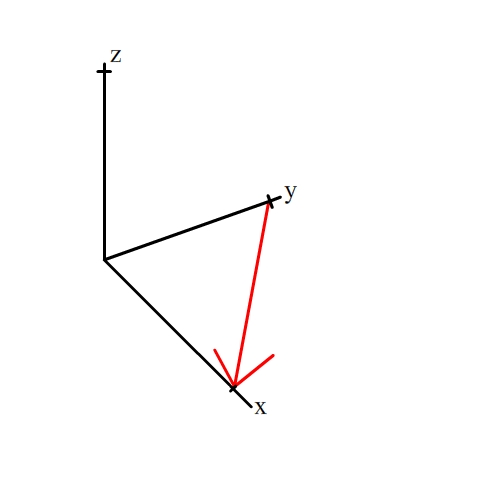
The planes (110), (001) and (111) are all in the zone [10], and so all contain that direction. (Direction shown by red arrow)
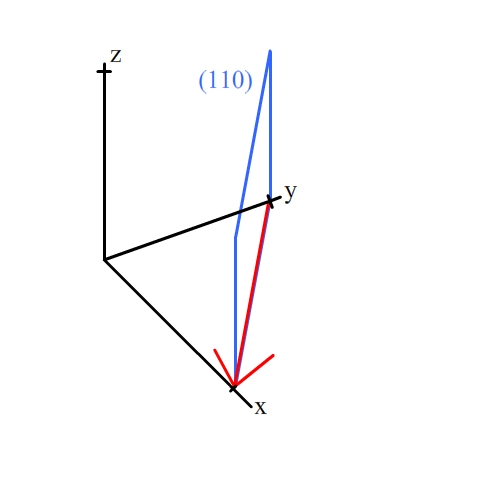
The planes (110), (001) and (111) are all in the zone [10], and so all contain that direction. (Direction shown by red arrow)
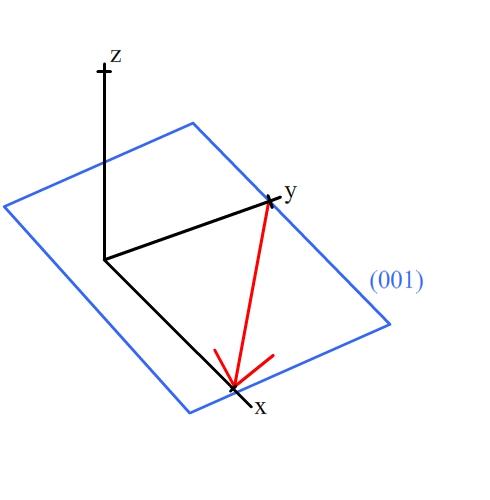
The planes (110), (001) and (111) are all in the zone [10], and so all contain that direction. (Direction shown by red arrow)
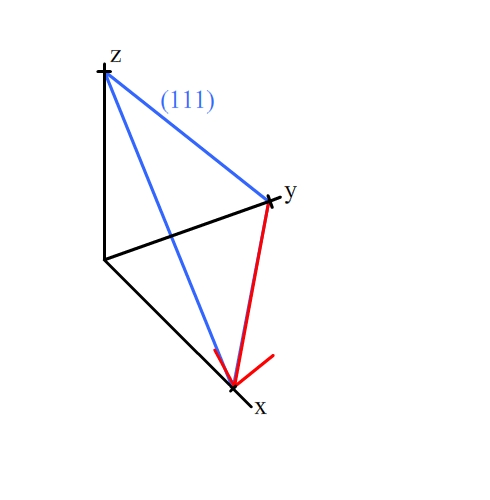
The planes (110), (001) and (111) are all in the zone [10], and so all contain that direction. (Direction shown by red arrow)
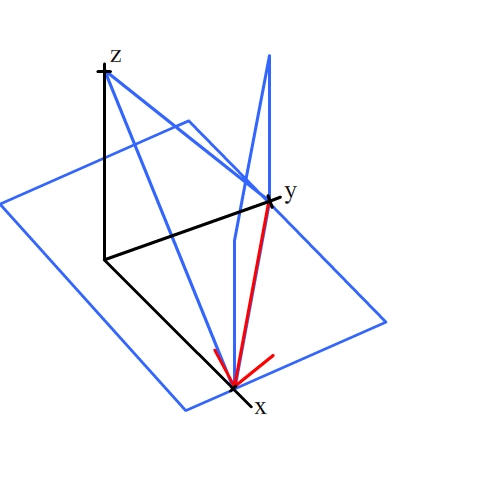
The planes (110), (001) and (111) are all in the zone [10], and so all contain that direction. (Direction shown by red arrow)