Plotting poles by the intersection of great circles

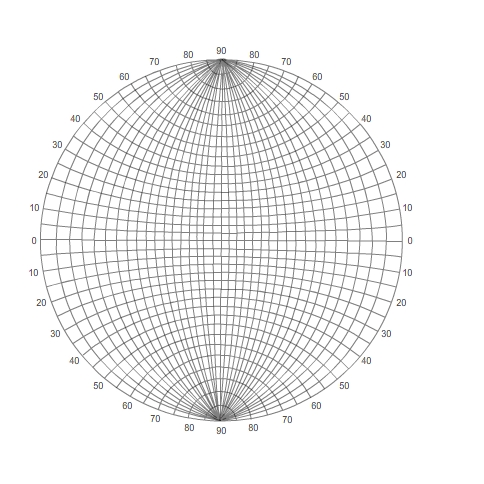
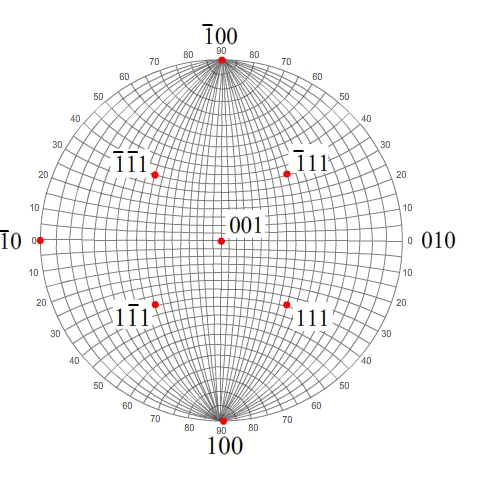
We have already seen certain poles on the Wulff net, so these will be assumed.

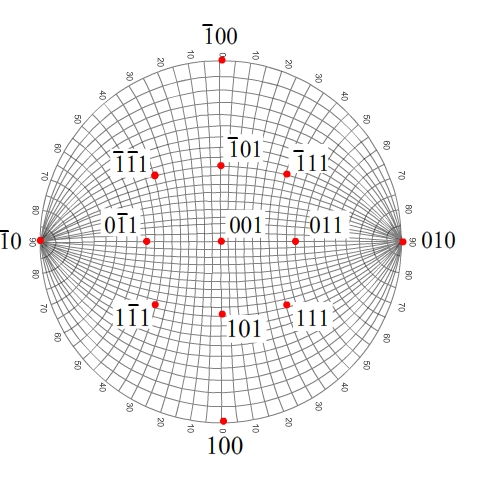
Suppose we wish to plot the poles of the form {101}. We need to find zones which contain these poles.

011 is in the same zone as 010 and 001, and is also in the same zone as 111 and 111.

So, we can plot the zone containing 010 and 001 by joining the two along a great circle.

So, we can plot the zone containing 010 and 001 by joining the two along a great circle.

We then join 111 and 111 along a great circle, and so plot the zone containing them.

We then join 111 and 111 along a great circle, and so plot the zone containing them.

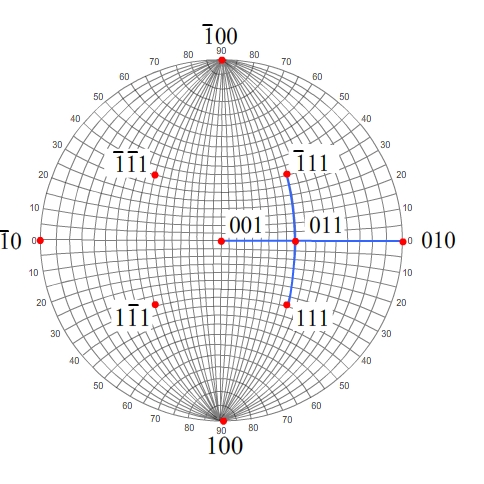
The 011 pole is at the intersection of these two zones.

This can be repeated for all the other relevant poles, with rotation of the Wulff net if necessary.

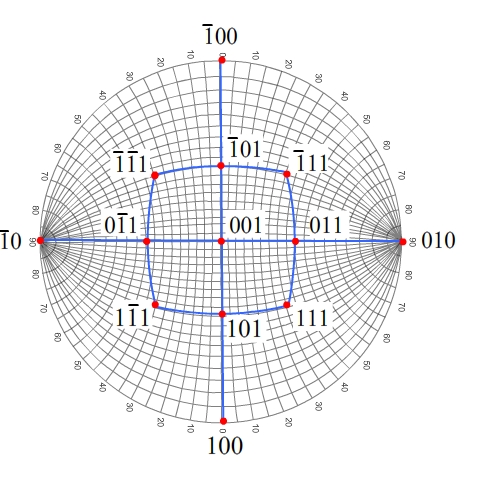
We can plot more general poles by making use of the Weiss zone law: (hU + kV + lW = 0).

For example, for the pole 121, we need to find the values of U, V and W, which produce a scalar product of 0 with the pole. Several possibilites come to mind, but the simplest are [101] and [111].

We therefore need to plot the great circles corresponding to the zones of [101] and [111]. Now, for cubic crystals, [hkl] will plot at the same position on the stereogram as the hkl pole. Therefore, for cubic crystals the required great circles also each represent the equivalent plane hkl in real space perpendicular to the plane normal represented by the pole hkl.

We do this by measuring 90° from the pole along the Wulff net, and then look at the great circle we have reached, i.e. for [101].

We then do the same for the [111] zone, with rotation of the Wulff net first.

The point where the two great circles cross defines the pole 121.

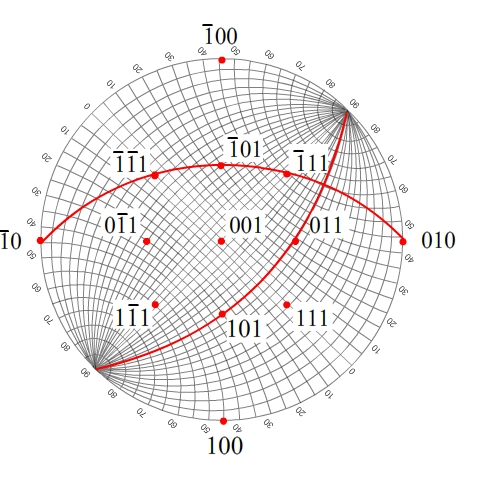
The point where the two great circles cross defines the pole 121.