NonCommercial-ShareAlike 4.0 International
https://creativecommons.org/licenses/by-nc-sa/4.0/
Plotting poles
by the
intersection of
a small circle
and a great circle
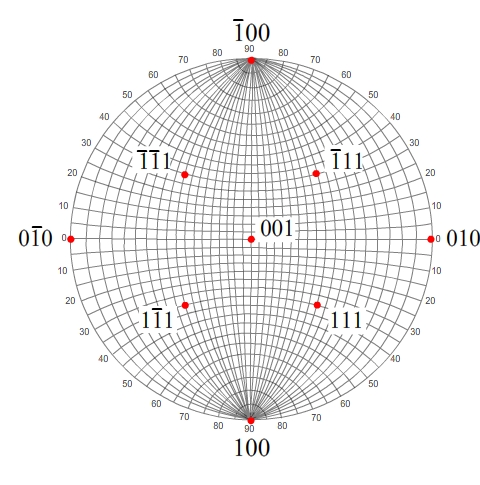
Suppose we wish to plot the pole 21
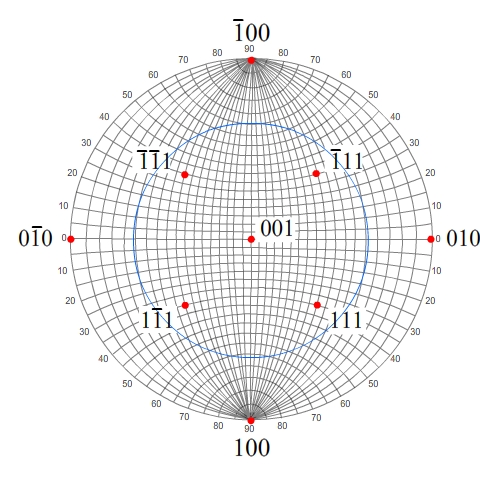
The angle between this pole and 001 is cos−1 (1/√6) which is 65.91°, so we draw the small circle with this angle around 001.
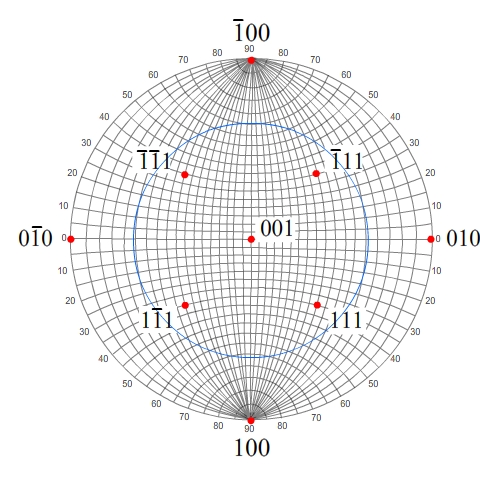
Method 1
We then construct the great circle passing through 001 and 21.
This great circle also passes through 20
and is a diameter of the stereogram. The angle between 20
and 010 is cos−1 (2/√5) = 26.57°. Therefore,
the relevant diameter is one which makes an angle of 26.57° with
the diameter passing through 00, 001 and
010.
Method 1
We then construct the great circle passing through 001 and 21.
This great circle also passes through 20
and is a diameter of the stereogram. The angle between 20
and 010 is cos−1 (2/√5) = 26.57°. Therefore,
the relevant diameter is one which makes an angle of 26.57° with
the diameter passing through 00, 001 and
010.
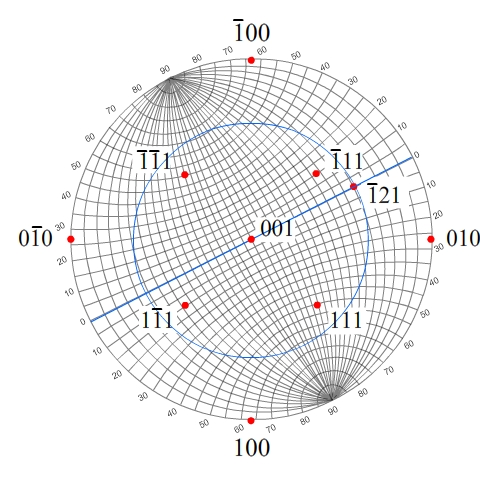
The small circle around 001 and the great circle we have just drawn intersect at 21 (and 11, but we can discount this as an answer because it would clearly be wrong).
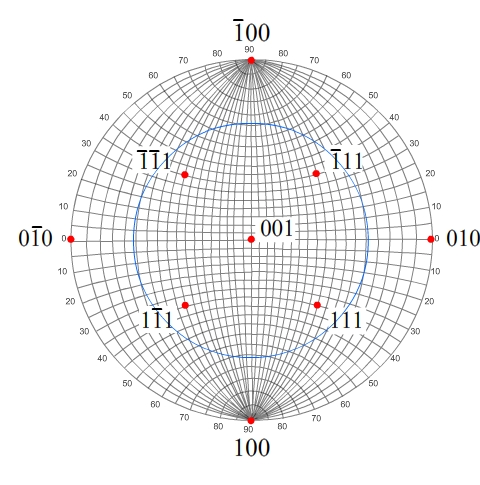
Method 2
21 lies on the great circle whose pole is
101.
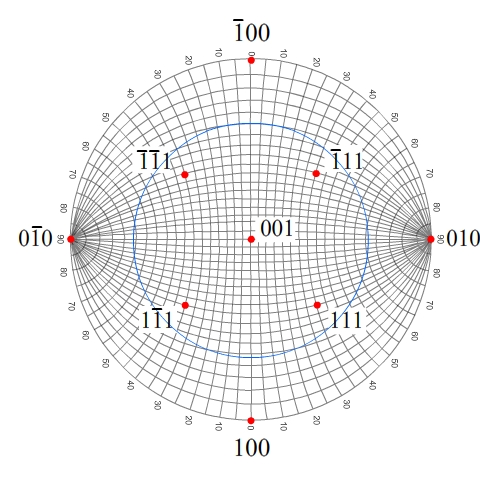
To plot this great circle, rotate the Wulff net by 90°.
Draw the 101 great circle. This great circle passes through 010, 21 ,1, 11 and 00, as shown.
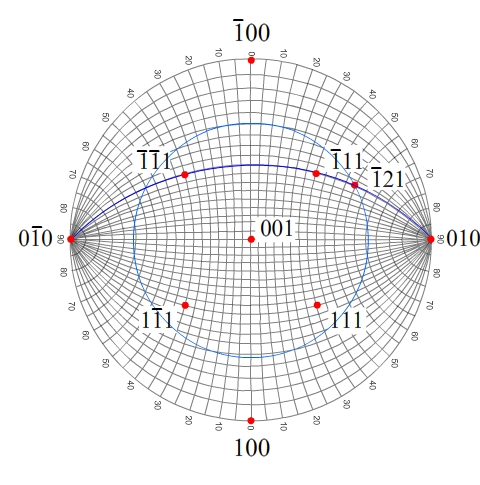
The small circle around 001 and the great circle we have just drawn intersect at 21 (and 1, but we can discount this as an answer because it would clearly be wrong).