Identifying poles and vector addition

If a and b are any two vectors in a plane, all other vectors lying in the plane are linear combinations of a and b, i.e. of the form

r = αa + βb

where α and β are numbers which are not necessarily integers

We can apply this system to the stereogram, by considering a great circle. This represents a plane in the material being examined. If we know the identity of poles in the great circle, we can find other poles in the great circle by linear addition.

010

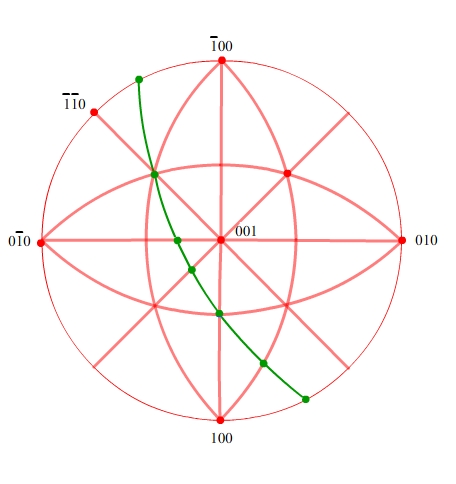
On this stereogram, the poles we already know are identified. There are a number of poles added that we don't know, designated with letters.

a

b

c

d

e

f

g

010

The identity of these poles can be found through the principle of vector addition just discussed. For example, 'b' is roughly half way between 001 and 110 on the Wulff net.

a

b

c

d

e

f

g

010

We might suppose that pole 'b' is composed of one unit of 110 and one unit of 001, giving its identity as 111. This is indeed the case, as can be proved by the intersection of great circles. It is therefore identified.

a

c

d

e

f

g

111

010

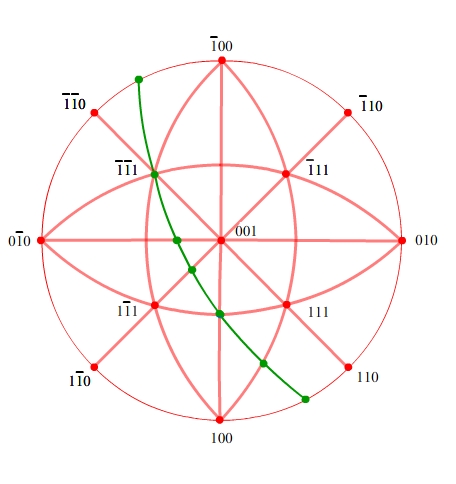
It is useful to plot other poles on the stereogram that are helpful for identification of unknown poles. These have been identified previously, and so can be added without difficulty.

a

c

d

e

f

g

111

010

We can now identify 'e', by the addition of 001 and 100, as 101.

a

c

d

f

g

101

111

010

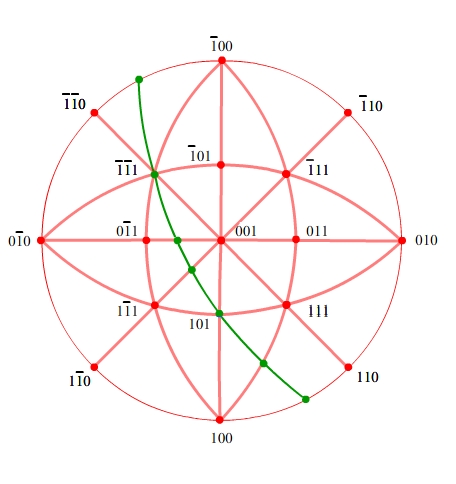
Other poles of the same form as 101 can be added.

a

c

d

f

g

010

'c' can be identified as a sum of 011 and 001. This means it could be 012, 013, 014 and others in that style. It is useful to have some more information. Since we know 'c' is in the green zone, it may be useful to identify that zone.

a

c

d

f

g

010

We've already identified two poles in the zone, so we have enough information to identify the zone itself. The poles in the zone are 101 and 111. We find the zone using the Weiss zone law.

a

c

d

f

g

010

Using the Weiss zone law, we find that the zone is:

i j k
1 0 1
−1 −1 1

i value: (0 x 1) − (1 x −1) = 1
j value: (1 x −1) − (1 x −1) = −2
k value: (1 x −1) − (0 x −1) = −1

The zone is therefore [121] or [121].

a

c

d

f

g

010

The pole 'c' is of the form hkl, but as we now know the zone, certain restrictions can be imposed on the plane. For the zone [121], using the Weiss zone law, we know:

- h + 2k + l =0

a

c

d

f

g

010

As the poles are potentially
012, 013, 014,
we can use the Weiss zone law already found to identify the plane. Comparing the various planes to:
− h + 2k + l = 0
allows us to see that
the plane 012 fits, with:
− (0 x 1) + (2 x −1) + 2 = 0.

We have therefore identified 'c'.

a

d

f

g

012

010

'd' is a sum of 001 and 111, so it could be: 112, 113, 114 etc. However, it has to lie in [121]. Therefore, we can identify the plane 'd' as 113.

a

f

g

012

113

010

'a' and 'g' both sit on the primitive circle, and are therefore in the [001] zone. This means that they take the form hk0. With the constraint that they are also in the [121] zone, it is easy to realise that they will be of the form 2h,h,0.

a

f

g

012

113

010

'a' is between 100 and 110, and so is obviously 210.
'g' is between 110 and 100, and so is obviously 210.
It can be noted that 'g' is diametrically opposite to 'a', and so is of the opposite sense to 'a'.

f

210

012

113

210

010

We have now identified 'e' and 'g', and so we can find 'f', as it is a linear sum of 'e' and 'g'. As a sum of 101 and 210, there are various possibilities: 311, 412, 521, etc. However, since the indices of the plane have to be a linear combination of 100 and 111, we can identify 'f' as 311.

210

012

113

311

210

010

This principle of identification can be applied to any system given enough time.

210

012

113

311

210