The theory predicts that the stiffness of rubber is proportional to the temperature.
The result of this is that, if the rubber is extended under a fixed load, it is likely to contract when it is heated (even after allowance is made for the thermal expansion).
This can be observed using the following apparatus:
|
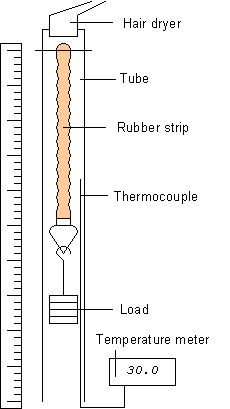
Diagram of apparatus |
Photograph of apparatus |
In the demonstration, a rubber strip is suspended inside a vertical Perspex tube, alongside a metre rule. The rubber strip is stretched by attaching a small load to the bottom end. The rubber is then heated using a hair dryer directed into the top end of the tube. A thermocouple is positioned inside the tube and connected to a digital meter that gives the temperature in degrees Celsius (which must be converted to K for use in the equations).
In order to verify the theoretical explanation, you will need to make five observations from the demonstration:
- initial unloaded length of rubber strip (L0)
- loaded but unheated length of the rubber strip (L1)
- initial temperature (T1)
- loaded heated length of the rubber strip (L2)
- final temperature (T2)
View video of the demonstration (3.62 MB) ... in separate window ... video alone
previous | next
© 2004-2013 University of Cambridge.