Entropy derivation

It is possible to treat quantitatively the entropy change on extending a polymer chain:

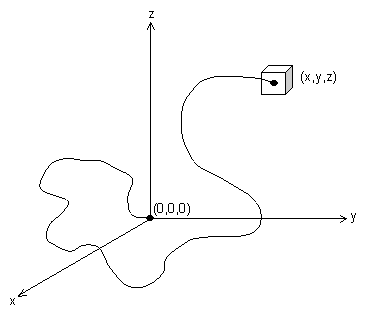
If one end of the chain is at (0,0,0), then the probability of the other end being at point (x,y,z) is:

\[p\left( {x,y,z} \right).dx.dy.dz = {\left( {\frac{b}{{\sqrt \pi }}} \right)^3}\exp \left[ { - {b^2}\left( {{x^2} + {y^2} + {z^2}} \right)} \right].dx.dy.dz\]

where

\[b = \sqrt {\frac{3}{{2n{a^2}}}} \]

a = bond length
n = number of links

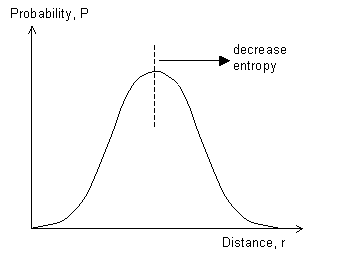
If we stretch the chain, so that the end is at a new location (x',y',z') such that (x'² + y'² + z'²) > (x² + y² + z²), then p(x,y,z) will decrease, leading to a decrease in entropy. The entropy is given by

S = k lnΩ

where Ω = total number of possible conformations leading to the same end position. Now

Ω = p(x,y,z,)

On stretching a chain, so that the initial end point (x,y,z) changes to (x',y',z') where

x' = λ_xx
y' = λ_yy
z' = λ_zz

the associated change in entropy is given by

\[\Delta S = k\ln \left( {\frac{{\Omega '}}{\Omega }} \right) = k\ln \left( {\frac{{p'}}{p}} \right)\]

ΔS = −kb² [((x')² − x²) + ((y')² − y²) + ((z')² −z²)]

ΔS = −kb² [(λ_x² − 1) x² + (λ_y²− 1)y² + (λ_z² − 1)z²]

In the unstressed state, with overall length r, we expect no preferential direction, so:

\[\left\langle {{x^2}} \right\rangle = \left\langle {{y^2}} \right\rangle = \left\langle {{x^2}} \right\rangle = \frac{{\left\langle {{r^2}} \right\rangle }}{3}\]

So, on average:

\[\Delta S = - k\left( {\frac{3}{{2n{a^2}}}} \right).\frac{{\left\langle {{r^2}} \right\rangle }}{3}.\left( {\lambda _x^2 + \lambda _y^2 + \lambda _z^2 - 3} \right)\]

From random walk theory,

〈 r² 〉 = na²

The entropy of a single chain segment can be multiplied by N (the no of chain segments) to give the total entropy change:

\[\Delta {S_{{\rm{tot}}}} = - \frac{1}{2}Nk\left( {\lambda _x^2 + \lambda _y^2 + \lambda _z^2 - 3} \right)\]