Theory

Although superconductivity was discovered as early as 1911, it was not until 1957 that Bardeen, Schrieffer and Cooper postulated a satisfactory explanation of the microscopic mechanism behind the effect.

Two Fluid Model

One of the first models to be formulated to start to describe superconductivity was the two fluid model. This model proposed that electrons within a superconductor appear as two different types, normal and superconducting, i.e. some of the electrons behave as they would in a normal metal and obey Ohm’s law, while others are responsible for the superconducting nature of the material. The crucial aspect of this model is that below Tc, only a fraction of the total number of electrons are capable of carrying a supercurrent. As the temperature is lowered, more of the electrons become the superconducting type while fewer remain as normal electrons.

In the two fluid model, normal and superconducting currents are assumed to flow in parallel when an electric field is applied. However, as the superconducting current flows with no resistance, it will carry the entire current induced by any electric field.

At the time the model was proposed there was no direct evidence for the existence of the superconducting electrons but it did help to explain some of the puzzling experimental observations.

London Conjecture

The next breakthrough in attempting to form an adequate theory came when two brothers, Fritz and Heinz London, made a useful connection between quantum mechanics and superconductivity. They correctly postulated that the diamagnetic properties of superconductors could be described by thinking of the material as a ‘giant atom’ with electrons orbiting around the edges producing the shielding currents responsible for the Meissner effect. This ‘giant atom’ could be produced by having all of the electrons in the body correlated in such a way that the entire specimen could be described by a single wavefunction.

If electrons flow in circulating currents around the surface of a superconductor, they will set up a magnetic field which is equal in magnitude but opposite in direction to the external field applied. This will cause the applied field to be completely expelled and result in the Meissner effect. However, the exclusion of the field from the interior cannot take place exactly up to the surface. This would cause a discontinuous jump in the magnetic field which would require an infinitely large current density at the surface which cannot occur. Thus the magnetic field penetrates the material over a thin surface layer.

The London equations quantitatively describe these screening currents and the magnetic field in the surface layer. In the simple one dimensional case of a plane perpendicular to the x axis and a magnetic field parallel to the z axis, the magnetic field decays exponentially over a characteristic length, λ.

\[{B_x}(z) = {B_0}{e^{\frac{z}{\lambda }}}\]

Detailed calculations using the London model show that λ is given by \[\lambda = \sqrt {\frac{{{m_{\rm{s}}}}}{{{n_{\rm{s}}}e_{\rm{s}}^2{\mu _0}}}} \]

where m_s, n_s and e_s are the mass, number density and charge of the supercurrent.

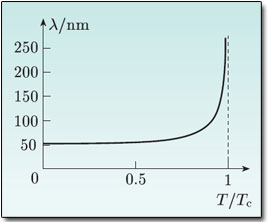
This characteristic length, λ, is known as the London penetration depth. A small value of the penetration depth implies that the magnetic field is effectively expelled from the interior of a macroscopic sample. The number density of superconducting electrons is dependent on temperature and means that penetration depth is as well. According to the London model, the penetration depth rises asymptotically as the temperature approaches Tc. Thus the field penetrates further and further as the temperature approaches T_c and does so completely above T_c.