Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Thermal Expansion and the Bi-material Strip Beam deflection during cantilever bending
Thermal Expansion and the Bi-material Strip AimsBefore you startIntroductionExperiment: Measurement of Young's modulusResults: Measurement of Young's modulusSimulation: Measurement of Young's modulusOrigin of thermal expansionThe bi-material stripExperiment: Estimating the boiling temperature of nitrogenResults: Estimating the boiling temperature of nitrogenExperiment: Measuring the thermal expansivity of polycarbonateResults: Measuring the thermal expansivity of polycarbonateSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Beam deflection during cantilever bending

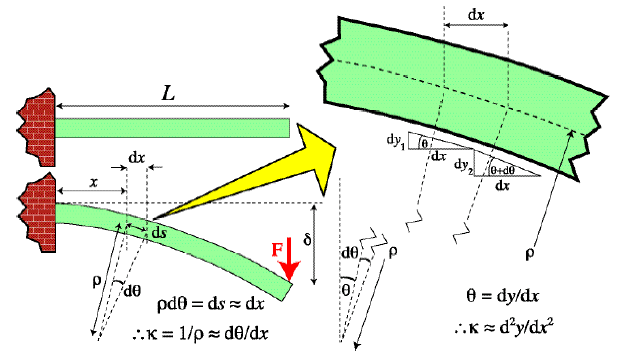
The beam curvature, κ, is approximately equal to the curvature of the line traced by the neutral axis, d2y/dx2 (see diagram below), so that

\[\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} = \kappa = \frac{M}{{EI}}\]

where M is the bending moment, E is the Young's modulus and I is the second moment of area. Applying this to the end-loaded cantilever beam, and taking the moment as positive when it generates a displacement in the downward direction (+ive y)

\[EI\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} = M = F\left( {L - x} \right)\]

where F is the load applied at the end of the beam.

Diagram of cantilever curvature

Approximation involved in equating beam curvature to the curvature of the neutral axis (Click on image for larger version)

The deflection is found by integrating this expression, using boundary conditions to establish the integration constants

\[EI\frac{{{\rm{d}}y}}{{{\rm{d}}x}} = FLx - \frac{{F{x^2}}}{2} + {C_1}\] \[{\sf{at }}\;x = 0, \frac{{{\rm{d}}y}}{{{\rm{d}}x}} = 0, \sf{thus}\; {C_1} = 0\]

\[EIy = \frac{{FL{x^2}}}{2} - \frac{{F{x^3}}}{6} + {C_2}\] \[{\sf{at }}\;x = 0, y = 0, \sf{thus}\; {C_2} = 0\]

The deflections along the length of the beam, and specifically at the loaded end, are thus given by

\[y = \frac{{F{x^2}}}{{6EI}}\left( {3L - x} \right)\] \[\delta = \frac{{F{L^3}}}{{3EI}}\]

PreviousNext