Factors affecting electrical conduction

Electrical conduction in most metallic conductors (not semiconductors!) is straightforward to approximate. There are three important cases:

Pure and nearly pure metals

For pure metals at around room temperature, the resistivity depends linearly on temperature.

\[ \rho_2 = \rho_1 [1 + \alpha(T_2 - T_1)]\]

However, at low temperatures, the conductivity ceases to be linear (superconductors are dealt with separately), and resistivity is related to temperature by Matthiesen’s rule:

\[ \rho(T) = {\rho _{{\rm{defect}}}}+ {\rho _{{\rm{thermal}}}} \]

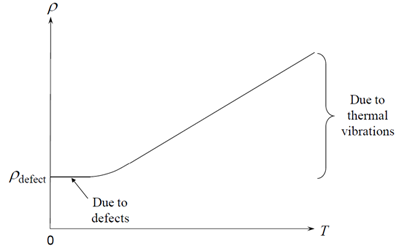
The low temperature resistivity ( \({\rho _{{\rm{defect}}}}\) )depends on the concentration of lattice defects, such as dislocations, grain boundaries, vacancies, and interstitial atoms. Consequently, it is lower in annealed, large crystal metal samples, and higher in alloys and work hardened metals. You might think that at higher temperatures the electrons would have more energy to be able to move through the material, so perhaps it is rather surprising that resistivity increases (and conductivity therefore decreases) as temperature increases. The reason for this is that as temperature increases, the electrons are scattered more frequently by lattice vibrations, or phonons, which causes the resistivity to increase. This contribution to the resistivity is described by ρ_thermal.

The temperature dependence of the conductivity of pure metals is illustrated schematically in the following simulation. Use the slider to vary the temperature, to see how the movement of the electrons through the lattice is affected. You can also introduce interstitial atoms by clicking within the lattice.

Alloys - Solid solution

As before, adding an impurity (in this case another element) decreases the conductivity. For a solid solution, the variation of resistivity with composition is given by Nordheim’s rule:

\[ \rho = \chi_{\alpha}\rho_{\alpha} +  \chi_{\beta}\rho_{\beta} +  C\chi_{\alpha}\chi_{\beta} \]

where C is a constant and CA and CB are the atomic fractions of the metals A and B, whose resistivities are ρA and ρB respectively.

Further, the difference in valency between the bulk lattice and the impurity atoms is proportional to the difference in resistivity -  Linde’s rule.

\[\Delta \rho \propto  (\Delta Z)^2 \]

where ΔZ is the difference in valence between the solute and the solvent.

Thus, solute atoms with a higher (or lower) charge than the lattice will have a greater effect on the resistivity.

Alloys- many phases

For an alloy where there are two or more distinct phases, the contributions simply contribute linearly to the total resistivity (though the effect of  many grain boundaries increases resistivity slightly).

\[ \rho = \chi_\alpha\rho_\alpha +  \chi_\beta\rho_\beta \]

The following animation illustrates Mattheisen’s rule, Nordheim’s rule and the mixture rule.