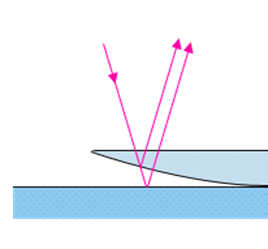
Surface topography
Flat surfaces polished to a mirror finish are not truly flat on an atomic scale, as shown below.
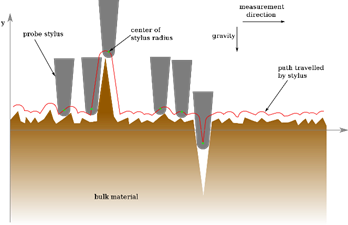
Surface roughness can be quantified using a stylus profilometer, where a fine stylus is moved over the surface. As it does so it rises and falls, giving the surface profile. This method will however produce some smoothing of the true profile, because of the finite dimensions of the stylus tip. This can be seen in the animation below. In the TLP for AFM, under the page called tip related artefacts, a similar concept is demonstrated.
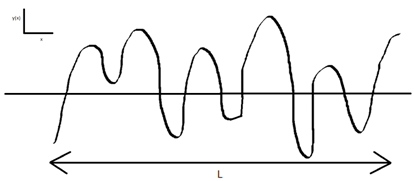
From a profilometer trace, the average roughness, \({R_{\rm{a}}}\), is defined as \({R_{\rm{a}}} = \frac{1}{L}\int\limits_0^L {{\rm{ }}\left| {y(x)} \right|} {\rm{ d}}x\)
where y(x) is the height of the surface at x above the mean line and L is the overall length of the profile. The mean line is defined by having equal areas of the profile above and below it. An exaggerated example is shown below.
For metals, polished surfaces typically have \({R_{\rm{a}}}\) values of 0.1–0.4 mm.
Contact between macroscopic ‘flat’ surfaces
Contact between surfaces occurs only at certain points, called asperities (circled below). Frictional force and wear originates at these asperities. These only cover a very small fraction of the total surface area - typically < 1%, but this will vary with factors such as the load on the surfaces. For contact between rubbery plastic surfaces and nominally smooth surfaces (e.g., polished glass), the contact area can approach that of the nominal area. Asperity contact can be either plastic (most metals) or elastic (most plastics and ceramics) and this cannot be altered by changes in the load.
Due to asperities the true area of contact is much less than the nominal area of contact. The true area of contact is related to the frictional force, so it is useful to be able to find an estimate for it. Click the link below for the derivation of an estimate for this and to see what determines whether asperities make contact elastically or plastically.
![]()
This concept of asperities is demonstrated by Newton’s rings:

A transparent rubbery polymeric phone casing was placed on a mobile phone with a glass back. In some regions concentric rings of different colours were visible - Newton’s rings. The images shown were obtained by viewing this with an optical microscope in reflected light mode.

The rings appear where there is dust between the polymer and the glass surfaces. There is substantial contact between the two surfaces here but there is an air gap where adjacent regions on the polymer and the glass are not in contact . This causes the appearance of Newton’s rings.

The formation of Newton’s rings can be understood by considering a plano-convex lens placed on a glass slide (effectively a single asperity). An air film of increasing thickness away from the contact point is formed. If white light is used concentric rings of different colours are seen, as is shown in the images.
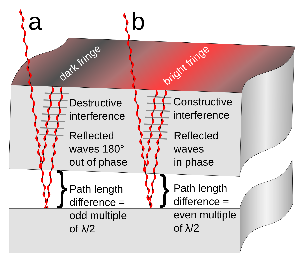
Newton’s rings are formed due to interference between light waves reflected from the top and bottom surfaces of the air film (see below). The bright rings are where the waves superpose in phase (path difference of a whole number of wavelengths) and the dark fringes are where the waves superpose in antiphase (path difference is an odd number of half wavelengths). See the birefringence pages in the liquid crystals TLP for a more in-depth explanation of a very similar concept. The rings are circular when the lens is perfectly spherical – which, as the images above show, can be a good first approximation of real situations.