Clausius-Clapeyron
The Clausius-Clapeyron equation in its most common form is used to determine the gradient of phase transition lines on a pressure-temperature plot.
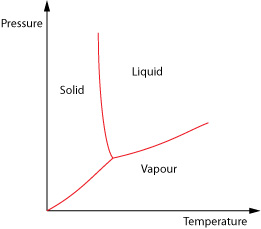
To derive the Clausius-Clapeyron equation we look at how pressure and volume vary with each other as a phase change occurs. We shall consider the liquid-gas change.
We need to form a heat engine cycle known as a Carnot Cycle. To do this we plot how the pressure and volume of the material vary when the temperature is held constant at two different temperatures (isothermals) and then add two adiabatic curves which show the relationship when no heat is allowed to flow in or out of the materials.
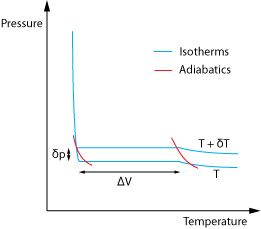
This forms the closed cycle which as we move round takes in and releases energy and is defined to have efficiency η, where;
\[\eta = \frac{W}{{\Delta H}} = \frac{{\delta T}}{T}\]
ΔH is the latent heat and is given as ΔH = T ΔS where ΔS is the associated change in entropy. The work done in the cycle, W, is given by its area, W = δp ΔV so;
\[\frac{{\delta T}}{T} = \frac{{\delta p\Delta V}}{{T\Delta S}}\]
and so as δT → 0 the gradient of the line showing the coexistence of the two phases on a plot of p vs T is given by;
\[\frac{{\delta P}}{{\delta T}} = \frac{{\Delta S}}{{\Delta V}} = \frac{{\Delta H}}{{T\Delta V}}\]
ΔH is the latent heat of the process, T is the temperature and ΔV is the associated volume change with the process.
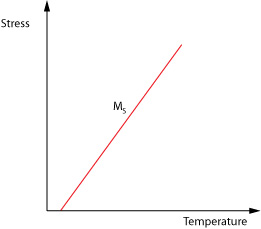
We however wish to know how the stress required to induce the martensitic change varies with temperature so we use the form;
\[\frac{{{\rm{d}}\sigma }}{{{\rm{d}}{M_s}}} = \frac{{ - \Delta H}}{{T{\varepsilon _0}}}\]
Where σ is the applied stress, Ms is the shifted temperature, and ε0 is the transformation strain along the direction of applied stress.

