Elasticity in Biological Materials (all content)
Note: DoITPoMS Teaching and Learning Packages are intended to be used interactively at a computer! This print-friendly version of the TLP is provided for convenience, but does not display all the content of the TLP. For example, any video clips and answers to questions are missing. The formatting (page breaks, etc) of the printed version is unpredictable and highly dependent on your browser.
Contents
Main pages
Additional pages
Aims
On completion of this TLP you should:
- Appreciate that many materials in living systems do not show Hookean elasticity.
- Understand the concept of J-curves and be familiar with examples of biomaterials that show this behaviour, in particular arterial wall.
- Understand how aneurysms arise in hardened arteries.
- Appreciate that some biomaterials, for example hair and spiders' silk, exhibit hysteresis, and understand how this can be essential to their performance and applications.
Before you start
Before beginning this TLP, you should understand the elasticity of rubber, including the concept of an entropy spring. Take a look at The Stiffness of Rubber TLP.
You should also be aware of how a tensile test is carried out. Take a look at the Introduction to Mechanical Testing TLP.
Introduction
As you will already know, many engineering materials, such as metals, show Hookean elasticity in which the tensile stress applied to a sample is directly proportional to the resultant strain. Within the range of Hookean elasticity, the stress-strain curves on loading and unloading are identical. Such linear elasticity is the usual assumption in engineering design. However, the elasticity of most materials in living systems is much more complicated.
In this TLP, you will learn that some biomaterials exhibit non-linear stress-strain curves. Mammalian skin, for instance, exhibits a J-shaped stress-strain curve, as do healthy arterial walls. Materials with J-shaped curves are usually tough, and have other advantages. For example, materials with different elastic behaviour such as S-shaped stress-strain curves are prone to elastic instabilities such as aneurysms when used for tubes under pressure.
This TLP also discusses viscoelasticity. Many biomaterials show time-dependent stress-strain curves. Associated with this, the loading and unloading curves do not superimpose on each other. Although deformation is elastic (i.e. recoverable), energy is absorbed during the deformation. This is particularly important in spider silk: when a fly hits the web its energy should be absorbed by the deformation of the web. If spider silk showed elasticity without energy absorption, then the web instead would act as a trampoline!
Hookean elasticity
For many materials loaded in uniaxial tension, the tensile stress on the material, σ, is directly proportional to the tensile strain , ε.
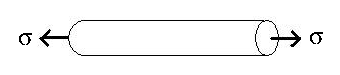
A sample loaded in uniaxial tension
The linear relationship between stress and strain is known as Hooke's Law,
σ ∝ ε
The constant of proportionality in this equation for simple tension is the Young Modulus of the material, E:
\[E = \frac{\sigma }{\varepsilon }\]
The Young Modulus of a material has values ranging from approx. 0.01 GPa for rubbers to approx. 1000 GPa for diamond.
Hooke's Law further states that the stress response of a material is independent of time and that the strain of a material disappears completely on removal of the applied stress (i.e. a Hookean material shows elastic deformation ).
This leads to a linear stress-strain curve with a gradient of E. Loading and unloading occur along the same curve.
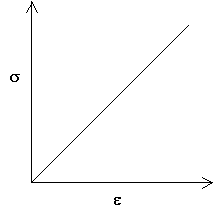
A stress-strain curve for a Hookean material
Most materials are Hookean only at small strains (typically less than 1%). Metals, for which fully elastic behaviour is only for very small strains (typically <0.2%), show Hookean behaviour. In this region, the extension is usually both linear and recoverable. At larger strains, extension is non-Hookean (i.e. either non-recoverable, or non-linear, or both).
Although many materials used in engineering applications show Hookean behaviour, only a few biomaterials approximate to it (wood and bone being the two most common). Many biomaterials exhibit a J-shaped stress-strain curve, but firstly, we shall consider the S-shaped stress-strain curve seen in rubbery materials.
S-shaped curves
S-shaped stress-strain curves occur in rubbery materials (lightly cross-linked polymers). Materials with S-shaped stress-strain curves are particularly susceptible to elastic instabilities, which are of interest in analysing phenomena such as aneurysms in arteries. The curves have the form:
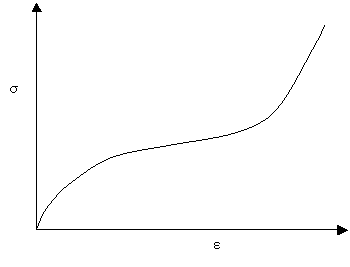
An S-shaped stress-strain curve
The initial part of this curve, where the stiffness decreases with increasing load can be predicted theoretically, by considering the rubber as an entropy spring, (shown in detail in The Stiffness of Rubber TLP). This treatment assumes that all extension occurs via conformational changes (i.e. that there is no bond stretching) and also assumes that the chain is composed of a series of joined links which are equally likely to lie in any direction (the random walk assumption).
Using the random walk assumption, the probability distribution for the end-to-end length of a polymer chain with a certain number of links can be obtained, and the Boltzmann expression (S = k lnW ) can be used to determine the change in entropy on extending the chain and moving it to a less probable conformation. The total entropy change can be found by multiplying the result for one chain by the total number of chain segments Nt.
If we assume that the extension occurs without significant change in the enthalpy, pressure, volume or temperature, then the change in Gibbs free energy (ΔG) can be related to the entropy change (ΔS) via the equation ΔG ≈ -TΔS. If deformation occurs only in the x direction then the force required for deformation is
\[F = \frac{{\partial \Delta G}}{{\partial x}}\]
and an expression for the stress required for a given extension (with the rubber in uniaxial tension) can be obtained.
If N is the number of chain segments per unit volume and λ is the extension ratio of the rubber, then the nominal stress for a rubber loaded in uniaxial tension is:
\[\sigma = kTN\left[ {\lambda - \frac{1}{{{\lambda ^2}}}} \right]\]
where k is the Boltzmann constant and T is the temperature.
This gives a stress strain curve of the form:
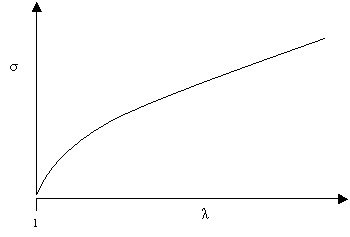
The theoretically predicted stress-extension curve for rubbery materials
Thus the theory predicts that the stiffness of rubber varies a little (particularly at low extensions), but that it tends to a limiting value at higher extensions. At lower extensions, the theoretical stress-extension curve is fairly similar to the S-shaped curves obtained experimentally. At extensions of λ = 4 the experimental and theoretical curves diverge, with much larger stiffness seen experimentally than predicted theoretically. This occurs because at larger extensions the assumptions of the model are no longer valid: the polymer chains are mostly aligned with the applied stress and so applying higher stress stretches strong intra-molecular bonds.
Aneurysms
Hardened and weakened arteries can show elastic instabilities such as aneurysms. A hardened artery can be modelled as a long cylindrical balloon, with radius r and internal pressure P. Consider the tension, T, in the polymer sheet as a function of the extension ratio, λ. The advantage of using T is that it allows us to ignore changes in the thickness of the polymer sheet, which may be considerable at large λ. The units of T are force/length.

For a cylinder of radius r, the pressure is related to the tension in the hoop direction, Thoop, by:
\[P = \frac{{{T_{{\rm{hoop}}}}}}{r}\]
An increased hoop tension for a given radius, or a decreased radius for a given hoop tension gives an increased pressure.
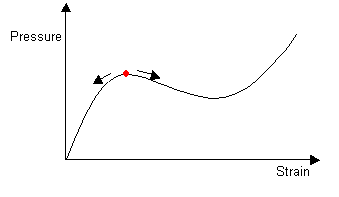
A plot of Thoop against λ for the balloon rubber would show a characteristic S-shaped curve, similar (but not identical) in shape to the stress - strain (σ — ε) curve:
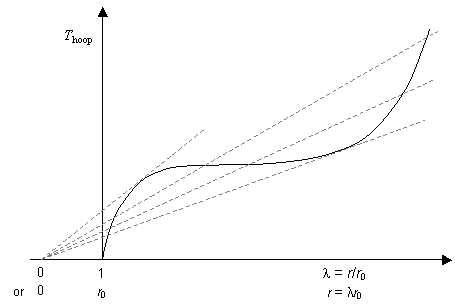
The gradients of the dashed lines are proportional to the pressure inside the balloon at the values of extension ratio (or radius) at which they cross the curve. This allows us to obtain the curve showing the variation of pressure with extension ratio:
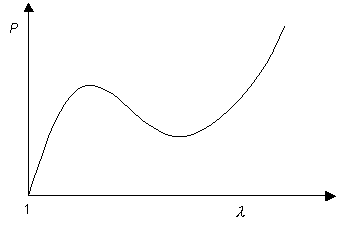
Although the tension in the balloon only ever rises with λ, it can be seen that this is not the case with pressure. The fact that there are regions of the graph for which
\[\frac{{{\rm{d}}P}}{{{\rm{d}}\lambda }} < 0\]
allows the occurrence of different radii at equal pressures, which leads to the formation of aneurysms.
This behaviour can be observed in modelling balloons, as shown in the next section.
Now consider Hookean behaviour:
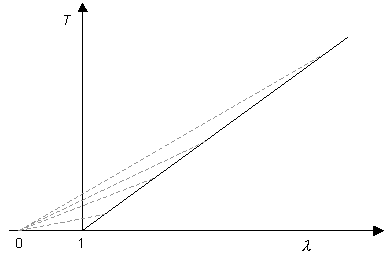
This then gives:
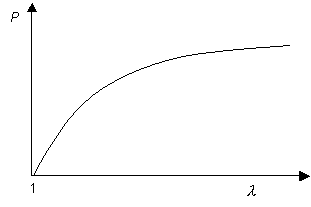
In this case, there is no region of
\[\frac{{{\rm{d}}P}}{{{\rm{d}}\lambda }} < 0\]
(although the gradient does tend to zero at large extension ratios). Thus if an artery exhibited Hookean elasticity, it should theoretically be stable against aneurysms, but only just, as the pressure inside the tubes is almost independent of its radius. However, since a normal artery exhibits natural variations along its length, Hookean behaviour in the arterial wall would not provide a strong safeguard against aneurysms. In fact, arteries exhibit J-shaped stress-strain curves as described later. For J-shaped curves dP/d λ is again always greater than zero but now does not tend to zero at large extension ratios. This provides greater stability against aneurysms.
Demonstration of aneurysms
As mentioned on the previous page, the behaviour of a modelling balloon can be used to provide a simple demonstration of an aneurysm. This is shown in the series of photographs below.
Initially, before any air is pumped into the balloon, it is completely deflated:
 |
(Click on image to view larger version) |
As the balloon is slowly inflated, it initially has one stable radius:
 |
(Click on image to view larger version) |
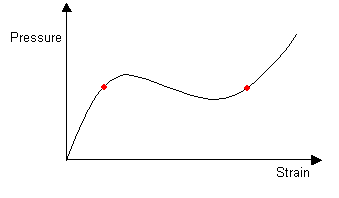
As air is blown into the balloon, the pressure continues to increase. When the balloon has an internal pressure equal to that at the maximum in the pressure-strain curve, an instability is introduced. The balloon develops an aneurysm, which greatly increases the internal volume and so the pressure goes down. The aneurysm grows to give a shape which is stable.
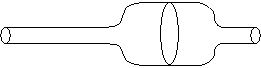
For the cylinder of small and large radius, and for the transition between the two, the local conditions of T and the curvature of the rubber are such as to correspond to a uniform internal pressure. Although the pressure is constant along the length of the balloon, two cylindrical radii are stable and so aneurysms are formed.
 |
(Click on image to view larger version) |
As more air is forced into the balloon the pressure within the balloon remains constant and the two radii stay the same size. The extra air is accommodated by the lengthening of the part of the balloon with greater radius. The lengthened aneurysm can also be split into two.
|
(Click on image to view larger version) |
(Click on image to view larger version) |
Aneurysms that form in arteries do not usually increase in length but instead increase spherically in radius until they burst. This is because the pressure-strain curve for hardened arteries does not have a local minimum after the maximum, but instead decreases continuously from the maximum.
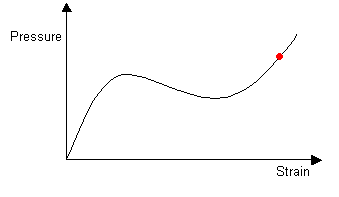
Once the balloon is completely inflated, it again has one stable radius. Further increases in pressure lead to uniform expansion.
 |
(Click on image to view larger version) |
The pressure inside the balloon as it inflates can be measured using a manometer. The balloon was fixed to the apparatus shown, and a pump was used to inflate the balloon at a constant rate.

As shown in The Stiffness of Rubber TLP, the difference in height of the two menisci in the manometer is proportional to the pressure inside the balloon. The videos below give a qualitative idea of how the pressure varies as the balloon is blown up. The pressure drop as the aneurysm forms and the constant pressure as the aneurysm lengthens are particularly obvious. The red lines in the video and on the picture show the initial position of the menisci.
Video showing the inflation of balloon on the manometer
Video giving a close-up of the manometer as the balloon expands
J-shaped curves
Descriptions of J-Shaped Curves
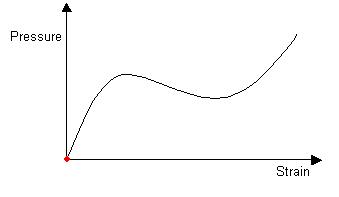
Many biomaterials exhibit the following type of stress-strain curve, which is known as a J-shaped curve:
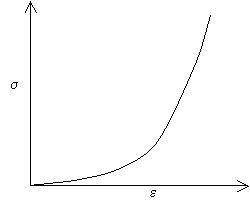
A J-shaped stress-strain curve
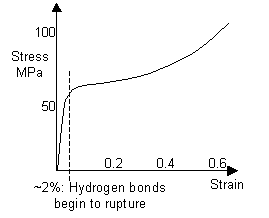
The curve shows that initially, small increases in stress give large extensions, however, at larger extensions the material becomes stiffer, and more difficult to extend. Mammalian skin and flesh are two of the many biomaterials that exhibit a J-shaped curve. If you pinch your earlobe and try to pull it downwards, you will see that initially it is quite easy to stretch the earlobe, but that at larger extensions it becomes more difficult to stretch.
Loading and unloading occurs along the same curve, i.e. the loading is completely reversible and elastic. This ensures that all the energy used in extending the system is returned once the load is removed. It is clearly important that there should not be too much energy absorption in arterial walls. The elastic properties of arterial wall are important not only to protect against aneurysms, but to smooth out variations in blood pressure and blood flow rate.
Advantages of J-shaped curves for biomaterials
J-shaped stress-strain curves cause biological membranes to be extremely tough, even though the fracture energy for many materials is not particularly high (around 10 kJ m-2). This toughness arises for the following reasons:
- The lower part of the J-shaped curve gives very large extension for low applied stress, so the shear modulus in this region is very low and so there is no mechanism whereby the released strain energy on fracture can be transmitted to the fracture zone.
- The material gets stiffer as the failure point approaches ensuring that very large extensions require large stresses, so that extensions which are likely to cause harm occur infrequently.
- Since the J-shaped curve is concave, the area under the curve up to a given extension is far lower than that for the equivalent Hookean curve meaning that the energy released in the fracture of a material with a J-shaped stress-strain curve is far lower than the energy released when an equivalent Hookean material fails. Since the release of energy drives crack propagation, a material that releases less energy on fracture is tougher.
- The J-shaped stress-strain curve does not lead to the elastic instabilities such as aneurysms which arise with S-shaped curves. Hence J-shaped curves are favoured for arteries.
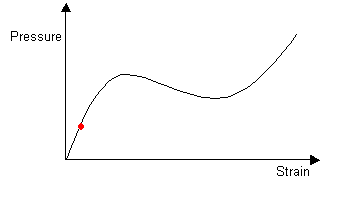
A J-shaped curve can be compared to an S-shaped curve in which the material has been pre-stressed, causing the effective origin of the graph to be further along the curve. This is shown below. Arteries are naturally pre-stressed as even the minimum blood pressure must be sufficiently positive to raise blood to the highest point of the body.
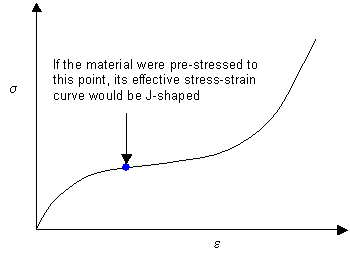
How Does the J-Shaped Curve Arise?
The J-shaped curve can arise at a number of different structural levels. For a J-shaped curve to arise, there must simply be the progressive recruitment of strain-resistant components. This can occur by the progressive alignment of polymer chains with the stress, and indeed, the stress-strain curve of a rubber is (at higher extensions) J-shaped. Many biomaterials are pre-stressed rubbery materials (i.e. in their neutral position they are still under tension). These rubbery materials, by virtue of being pre-stressed, show only J-shaped behaviour. A similar effect occurs in materials that contain fibres in a soft matrix. Initially the stress acts only against the soft matrix, but with time the fibres align in the direction of the stress and so further pulling works against the stiffer fibres. This effect is used in arterial walls, where the collagen fibres act as the stiffer fibres. (More information on the structure of arterial walls.)
Examples of Materials With J-Shaped Stress-Strain Curves
Textile materials provide some non-biological examples of materials with J-shaped stress-strain curves. Knitted materials and woven fabrics pulled at 45° to the warp and weft have J-shaped curves and are thus quite tough. Knitted fabrics usually fail by unravelling not by tearing, and when woven fabrics tear it is usually along the warp and weft directions, even though these directions are those in which the force is aligned with the strong threads.
Many biological soft tissues, show J-shaped stress-strain curves. Skin and arterial walls have already been cited as examples. Viscid spider silk (the capture threads) is a further example. At low strains, both collagen and tendon show J-shaped curves, in fact, the toughness of raw meat is due to the presence of collagen fibres within the meat. On cooking, the collagen disintegrates, and the meat becomes tender.
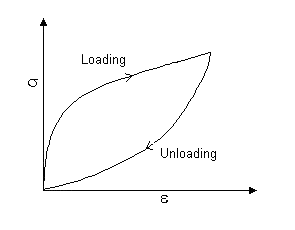
Viscoelasticity and hysteresis
Some biomaterials show a time-dependent elastic behaviour. Although, in the elastic regime, the strain is recoverable, the stress-strain curve is not the same for loading and unloading. Such materials instead exhibit viscoelasticity, involving both elastic and viscous components, which at normal loading and unloading rates leads to hysteresis. A typical hysteresis curve is shown below, and the energy absorbed during one loading-unloading cycle is given by the area within the loop. The shape of the loop depends on the rates of loading and unloading (unlike normal time-independent elasticity).
Hair
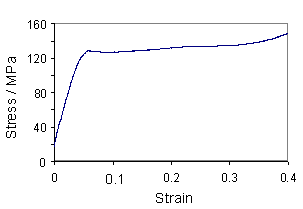
The effect of hysteresis can clearly be seen in hair. Hair consists of keratin, which is a type of protein. There are two main forms of keratin: α-helices, which are found in hair, and β-sheets. As the names suggest, α-helical keratin (also known as α-keratin) contains keratin molecules arranged in helices and held in place by hydrogen bonds, whereas β-sheet keratin (also known as τ-keratin) contains keratin molecules arranged in flat sheets, in which adjacent molecules are antiparallel due to more favourable interactions between side-groups.
As hair is stretched, the hydrogen bonds between the α-helices rupture, causing the helices to unravel to form β-sheets. The curve for human hair, and a curve obtained for a horse hair from a violin bow are shown below.
|
Stress-strain curve of a human hair (Structural biomaterials, Vincent) |
Measured stress-strain curve of a horse hair from a violin bow |
When the stress on the hair is removed, the helices re-form over time, and since the unravelling of α-helices to form β-sheets is a high-energy-absorbing process, a large area is contained within the hysteresis loop. As a result, this energy is unavailable for fracture, giving a high toughness. This is particularly important for hooves and horns, which are also made up of keratin.
The following graph shows experimentally measured stress-strain curves for human hair, dry horse hair (as used in violin bows) and replasticized horse hair (the same type of horse hair but soaked in water).
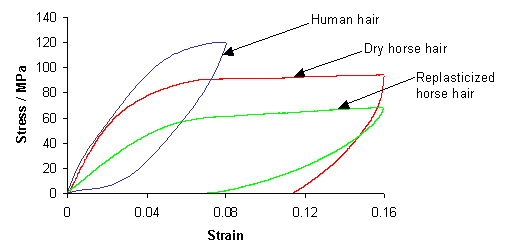
As you can see, the replasticized horse hair requires less force to stretch than the dry horse hair (for the same extension). This is because the presence of the water allows the unravelling and reravelling of the helices to occur more easily.
If the human hair had been stretched to a higher strain, its hysteresis curve would look more like this:
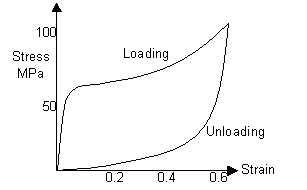
Spiders’ silk
There are two main types of silk: spiders’ silk and the silk produced by silk worms. Both types have very good mechanical properties, are durable and readily available, and both form fine threads (typically about 1 μm in diameter) that are biodegradable and biocompatible, making them ideal for use as suture materials.
The two silks are proteins and are very similar in composition: they are made up of similar proportions of the same amino acids. However, the sequence of these amino acids in spiders' silk is much less regular than that from silk worms, impeding the formation of crystallites (micelles) and making it much more extensible.
Spiders produce silk in several different glands, each of which produces silk for a different purpose (wrapping prey, producing drag lines, forming frame threads and capture threads etc). Slightly above the concentration of protein found in the gland, the silk proteins form a liquid crystalline phase. This liquid crystalline phase is formed as the silk passes through the duct leading to the spinnaret, and the silk crystallizes as it passes through the spinnaret itself to form an insoluble β-sheet. The higher the draw ratio through the spinnaret, the higher the orientation of the fibres.
Frame threads contain well-aligned molecules, and are highly crystalline, dry and relatively thick. In contrast, capture threads contain less-aligned molecules, and are less crystalline, plasticised, relatively thin, and exist as coiled fibres within an 'aqueous glue' layer.
The coefficient of restitution, or resilience, describes the fraction of energy returned elastically and can vary by a very large amount, as seen in the table below.
| Resilin | Found in the wing hinges of insects | 97% |
| Collagen | Found in tendons, ligaments, skin etc. | 93% |
| Elastin | The main elastic protein of vertebrates | 76% |
| Viscid silk | Capture threads | 35% |
Capture threads are made from a material known as viscid silk and are used to capture prey. Viscid silk has a very low coefficient of restitution, making it ideal for absorbing the energy of an insect flying into the web (instead of catapulting it away!). Its high strength also helps to ensure that the web is not destroyed upon impact. The hysteresis curve for viscid silk is shown below.
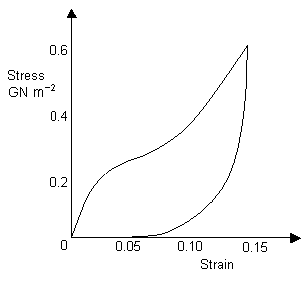
Silk from silkworms

silkworm starting spinning a cocoon © Michaal Cook www.wormspit.com
Silk is used in nature by silk worms to form their cocoons, and so must be strong and not easily breakable, as this would kill the silkworm, preventing it maturing into a moth and reproducing. Silkworms originate from China, India and Japan, and have been used by humans to make silk since at least 3,000 BC. Although silkworms only live for two months, they manage in this time to eat roughly 30,000 times their initial weight. It is estimated that 2,500 to 3,000 cocoons are needed to make just one yard of silk fabric, so despite silk being an excellent material for making fibres it is also expensive to produce.
Summary
In this TLP the elastic properties of biological materials were studied. You will have learnt that few biological materials exhibit Hookean behaviour either because they do not have linear stress-strain curves, or because they do not have reversible stress-strain curves.
Many biomaterials show J-shaped curves and the reasons why these arise were discussed, in terms of material structure. The S-shaped curve has been covered, and concepts such as the entropy spring introduced in The Stiffness of Rubber TLP have been revised. You will have seen that S-shaped stress-strain curves lead to elastic instabilities such as aneurysms, and that this can be demonstrated experimentally, using cylindrical balloons.
Horse hair, human hair and spider silk are examples of materials which show viscoelasticity and tensile tests were carried out on human hair and horse hair. You should now be aware of the structure of hair and spider silk and the reasons for their low coefficient of restitution.
Questions
Quick questions
You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!
-
What type of stress-strain curve does a normal arterial wall show?
-
What type of stress-strain curve does natural rubber show?
-
What type of stress-strain curve do metals at small extensions show?
-
What type of stress-strain curve does bone show?
-
What type of stress-strain curve does skin show?
Deeper questions
The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.
-
Estimate the coefficient of restitution (sometimes known as the resilience) of a human hair using the hysteresis curve below:
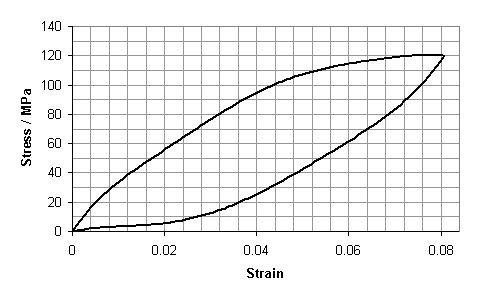
-
Why are hairs used in violin bows?
-
A fly of mass 30 mg hits a spider's web at 0.8 m s-1 and is stopped by two capture threads each of diameter 0.7 micrometres and length 5 cm. Calculate the maximum tensile strain in the threads, assuming that the tensile loading curve of the capture threads can be approximated as a straight line with gradient 0.1 GPa.
-
(.. continuation from previous question) Given that the coefficient of restitution of a capture thread is 35%, calculate the total energy dissipated in the two threads.
-
(.. continuation from previous question) Since the threads are very thin, this energy would easily be dissipated as heat to the surrounding air. However, supposing that the process is adiabatic (no heat transfer occurs), estimate the temperature rise that would occur. The density of viscid silk is 1500 kg m-3 and the specific heat capacity is 1400 J K-1 kg-1.
-
(.. continuation from previous question) Comment on the effects of using cables with a large diameter made of viscid silk, for example to decelerate aircraft landing on carriers.
Going further
Books
- S Vogel, Comparative Biomechanics: Life’s Physical World, Princeton University Press, 2003.
- JE Gordon, The Science of Structures and Materials, Scientific American Books, 1988.
- JFV Vincent, Structural Biomaterials, Princeton University Press, 1990.
Websites
- Mechanical
properties of keratin
A site maintained by Richard Bonser about the mechanical properties of keratin, with particular reference to the mechanical properties of feathers. - Silk
biomechanics
An article on the American Museum of Natural History website.
Extension ratio
The extension ratio, λ , is a measure of how much an object has been extended. For an object with initial length l0 and extended length l,
$$\lambda = {l \over {{l_0}}}$$
and so λ = 1 + strain
The extension ratio is commonly used when discussing the mechanical properties of rubber, with tensile strain being used in other applications. In this TLP, both extension ratio and strain are used.
Arteries
Arteries consist of layers of oriented elastin interspersed with randomly oriented collagen (in a matrix of water and polysaccharides). This complex structure gives arteries a strong J-curve.
Elastin is the main elastic protein of vertebrates. It is plasticised by water and has a coiled coil structure. Its elasticity has two components: one obeying ordinary rubber elasticity theory, and the second resulting from an elastic restoring force due to free energy changes associated with the hydration of non-polar groups at the centre of a deformed molecule. Collagen is a protein that forms characteristic fibres in most of the animal kingdom. It is widely found in the human body, including in bone, skin, tendon, ligament and cartilage, as well as in artery. A single collagen molecule shows a left-handed helix, and three of these coil together to form the collagen triple helix, tropocollagen. These pack to form fibrils, which are good stress-transmitters.
The elastin fibres are aligned around the circumference of the artery, and
as the artery is strained, the randomly oriented collagen fibres begin to straighten
and align. More become load-bearing and the Young's Modulus increases. Due to
the initial random orientation of the collagen fibres, some fibres are stressed
and yield even at low strains, giving toughness, but even at high strains not
all fibres are load-bearing, giving a high failure strain. This effect is also
observed in skin, which consists of a random feltwork of collagen and elastin
fibres. In an artery, the elastin fibres deflect longitudinal crack growth and
help to counteract the high hoop stresses (in the wall of a pressurised cylindrical
tube, the hoop stress is twice the longitudinal stress). The overall properties
of an artery are elastic, which allows energy to be returned to the blood.
Academic consultant: Lindsay Greer (University of Cambridge)
Content development: Jessica Gwynne, Sarah Parker and Stuart Fraser
Photography and video: Brian Barber and Carol Best
Web development: Dave Hudson
This TLP was prepared when DoITPoMS was funded by the Higher Education Funding Council for England (HEFCE) and the Department for Employment and Learning (DEL) under the Fund for the Development of Teaching and Learning (FDTL).
Additional support for the development of this TLP came from the UK Centre for Materials Education.