Coping with a scatter in strength
The Griffith expression shows that the stress required for failure in tension is dependent on the size of the largest flaw, c, according to \(1/\sqrt c \).
In very brittle materials the flaw sizes cannot be easily measured, so it is sometimes impossible to calculate a minimum strength.
Using a method by Weibull, we can then find the chance of survival of a sample as a function of applied stress. We can then extrapolate back to an acceptable probability of failure and find the corresponding stress.
The linked derivation gives a relationship of
$$\ln \ln {1 \over {{S_n}}} = m\ln \sigma - (m\ln {\sigma _{\rm{o}}} + \ln N)$$
where Sn is the probability of survival, and σ is the fracture stress.
We can treat our results from the tensile of testing of paper with Weibull statistics:
Using Weibull’s method
To determine the survival probability associated with each stress we start by testing some samples, in this case the graph paper used in the first video of the TLP. The following table shows all the collected data, and the calculated values needed:
| n | UTS | Sn | ln ln (1/Sn) | ln σ |
| /MPa | ||||
| 1 | 21.28 | 0.07 | 0.9704 | 16.8733 |
| 2 | 20.86 | 0.14 | 0.6657 | 16.8531 |
| 3 | 20.20 | 0.21 | 0.4321 | 16.8213 |
| 4 | 20.20 | 0.29 | 0.2254 | 16.8211 |
| 5 | 20.12 | 0.36 | 0.0292 | 16.8173 |
| 6 | 19.30 | 0.43 | -0.1657 | 16.7755 |
| 7 | 19.03 | 0.50 | -0.3665 | 16.7615 |
| 8 | 18.87 | 0.57 | -0.5805 | 16.7531 |
| 9 | 18.53 | 0.64 | -0.8168 | 16.7347 |
| 10 | 18.49 | 0.71 | -1.0892 | 16.7330 |
| 11 | 18.11 | 0.79 | -1.4223 | 16.7122 |
| 12 | 18.10 | 0.86 | -1.8698 | 16.7112 |
| 13 | 17.74 | 0.93 | -2.6022 | 16.6912 |
From Weibull treatment of graph paper test.xls
Remember that Sn is the probability of survival at a given stress, given by
$${S_n} = {n \over {{n_{\rm{T}}} + 1}}$$, where nT is the total number of samples and σ is the fracture stress of the sample.
The data has been ordered with the highest strength being 1, and the lowest numbered down to n.
When we plot the graph of ln ln (1/Sn) vs ln (UTS), we get the following:
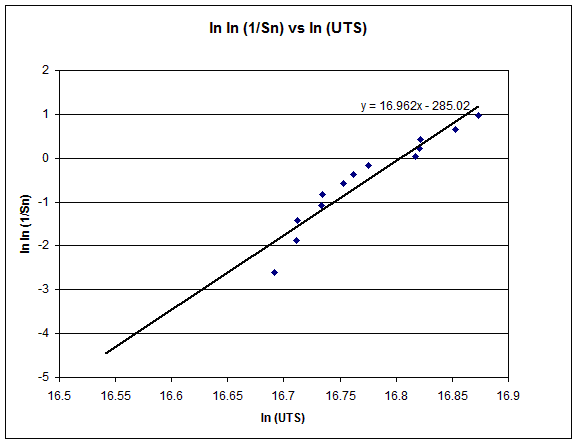
From Weibull treatment of graph paper test.xls
We can then read off the graph for various values of Sn. For instance if we wanted a 99% chance of survival, we read off from –4.60 on the y axis, which corresponds to 15.1MPa.
A fully interactive version of this spreadsheet and graph tool can be downloaded here.

