Representing Texture 2
Crystal Orientation Distribution Function (CODF)
As previously mentioned, pole figures do not give information about the orientation of a particular crystal relative to another. More information can be gathered from a CODF. CODFs are constructed by combining the data from several pole figures. This requires intensive use of mathematics. More details can be found in the references listed in the Going further section.
CODFs describe the orientation of each crystal relative to three Euler angles (φ,ψ, and θ). The Euler angles define the difference in orientation between the crystal axes and the deformation axes (i.e. the RD, the ND and the TD).
One convention for Euler angles (and the convention described here) is known as the Roe convention. An alternative convention can be used where the θ-rotation occurs about the x1 direction; this is known as the Bunge convention. These two conventions are related by:
ψRoe = ψ1,Bunge – π/2
θRoe = φBunge
φRoe = ψ2, Bunge + π/2
A single crystal is completely described by a point in a cube with axes of φ, ψ and θ. This cube is referred to as Euler space and is often shown as a series of cross-sections.
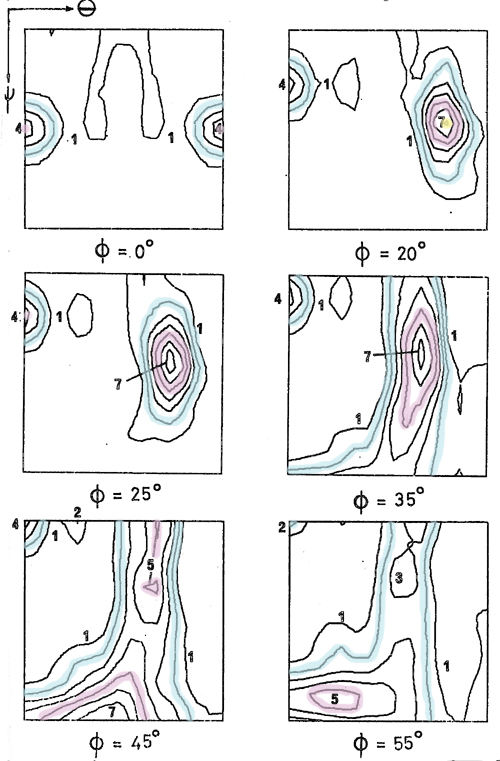
These sections of a CODF are for a steel sheet cold-rolled to an 80% reduction in thickness. Any values of φ between 0° and 90° can be used to produce the sections. In the image above, the values of φ that have been chosen are: 0°, 20°, 25°, 35°, 45°, and 55°. The contours of the sections make up part of a three-dimensional surface in Euler space as seen in the following animation. The highlighted contours on the sections correspond to the similarly coloured surface in the 3D plot below. The area of highest density and hence strongest texture is bound by the yellow surface centred around φ = 26.6°, ψ = 39.2°, and θ = 65.9°. The original figure can be found in D.J. Goodwill Ph.D. thesis, University of Cambridge (1972) – The relationship between texture and properties of steel sheets.
Texture diagrams such as those produced by Davies, Goodwill, and Kallend (1971) (See Going further) can be used to identify the texture present. In this case it is (11)[01]. (11) describes a plane which is orientated parallel to the plane of the sheet, while [01] is a direction parallel to the rolling direction.


