Interdiffusion
Kirkendall Effect
We will now consider a diffusion couple: that is two semi-infinite bars of materials A and B joined together, such that material diffuses from A to B and from B to A. This is interdiffusion. We can assume that during this process the dimensions of the total bar remain the same, and that no porosity develops.
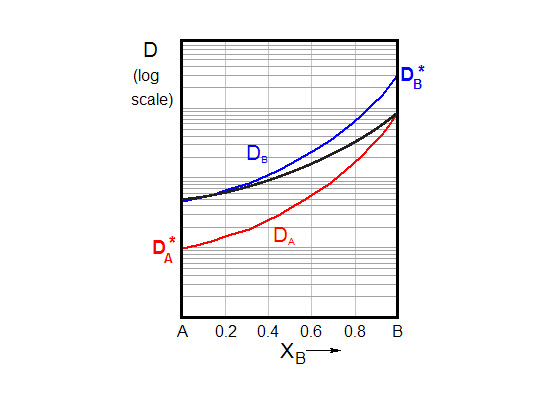
The diffusivity of the two materials will not be the same: We will assume that DB > DA. This would, in theory, lead to a net drift of atoms towards A; the diffusion couple would appear to move to one side as you look at it!
We know, however, that this does not happen. In practice there is a lattice drift from left to right, so that the bar remains stationary in the laboratory frame. This lattice drift can be detected by placing inert markers at the interface between the two materials, and observing their drift as the two materials interdiffuse. This is known as the Kirkendall effect.
Darken Regime
The Darken equations are Fick's laws adapted for substitutional diffusion, by the motion of vacancies. The equations can be found by equating the flux of atoms and the flux of vacancies within a diffusion couple, and finding the velocity of the lattice drift.
This gives the following equations, known as the darken equation:
\[{J_A}' = - \tilde D\left\{ {\frac{{\partial {C_A}}}{{\partial x}}} \right\}\]
Where \({\tilde D}\) is the interdiffusion coefficient, such that
\[\tilde D = {X_A}{D_B} + {X_B}{D_A}\]
This and the expression for the lattice drift velocity below are known as the Darken relations:
\[v = \frac{1}{{{C_0}}}\left( {{D_A} - {D_B}} \right)\left\{ {\frac{{\partial {C_A}}}{{\partial x}}} \right\}\]
The derivation for this equation is long, and can be found here
Nernst-Planck Regime
The Darken relations only apply if there are sufficient, and efficient, sinks and sources for vacancies, and if diffusion is slow enough, and over large enough distances, that stresses have sufficient time to relax such that no porosity results.
If the sinks and sources are not sufficient, or if the diffusion distance is small (such as in a multilayer), stresses build up, and porosity forms. The Darken regime no longer applies, and the system moves into the Nernst-Planck Regime:
\[\frac{1}{{\tilde D}} = \frac{{{X_B}}}{{{D_A}}} + \frac{{{X_A}}}{{{D_B}}}\]
It is often useful to relate the Darken regime to series conduction, and the Nernst-Planck regime to parallel conduction. In the Darken regime the diffusivity is controlled by the fastest component; in the Nernst-Planck regime it is limited by the slowest.

