• Notched bar in plane bending
Lower-Bound:
The area immediately under the notch, above the neutral axis is in tension σ = 2k. The area below the neutral axis is in compression σ = 2k.
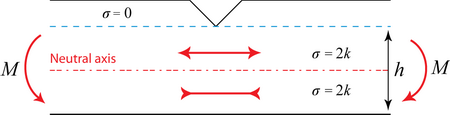
where:
h = thickness of slab beneath the notch.
\(2k.\) \(\frac{h}{2}\)\(.b\) = magnitude of forces in tensile and compressive regions.
\(\frac{h}{2}\) = distance between the two.
Equating the couples, \(M = \) \(\left( {2k.\frac{h}{2}.b} \right)\) \(\frac{h}{2}\) = \(0.5k{h^2}b\)
Upper-Bound:
Assume failure occurs by sliding around a ‘plastic hinge’ along a circular arc of length l and radius r.
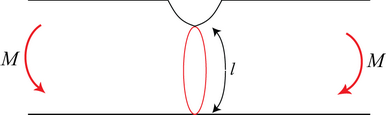
If the rotation is δθ, the internal work done \( = k.lb.r\delta \theta \) along one arc.
External work = Mδθ by one moment.
\[ \Rightarrow M = klbr\]
where no assumptions have been made regarding l and r.
The upper bound theorem states that whatever values are taken for l and r will lead to an upper bound. Clearly we wish to find the lowest possible value.
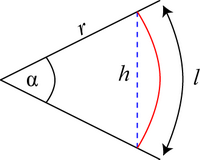
From the above geometry,
\(l = r\alpha \) and \(r = \) \(\frac{h}{{2\sin {\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/
{\vphantom {\alpha 2}}\right.\kern 2pt}
\!\lower0.7ex\hbox{$2$}}}}\)
\[ \Rightarrow M = \frac{{k{h^2}b}}{4}\frac{\alpha }{{{{\sin }^2}{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern 1pt} \!\lower0.7ex\hbox{$2$}}}}\]
and so to find the lowest possible value of M, we minimise the function \(\frac{\alpha }{{{{\sin }^2}{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/
{\vphantom {\alpha 2}}\right.\kern 1pt}
\!\lower0.7ex\hbox{$2$}}}}\)
Let \(Y = \) \(\frac{\alpha }{{{{\sin }^2}{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern 1pt} \!\lower0.7ex\hbox{$2$}}}}\)
\(\frac{{{\rm{d}}Y}}{{{\rm{d}}\alpha }} = \frac{1}{{{{\sin }^4}{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern 1pt} 2}}}\left\{ {{{\sin }^2}\frac{\alpha }{2} - 2\frac{\alpha }{2}\cos \frac{\alpha }{2}\sin \frac{\alpha }{2}} \right\}\)
= 0 when \(\sin \frac{\alpha }{2} = \alpha \cos \frac{\alpha }{2}\)
\[ \Rightarrow \tan \frac{\alpha }{2} = \alpha \]
\[ \Rightarrow M = \frac{{k{h^2}b}}{4}.\frac{1}{{\sin {\raise0.5ex\hbox{$\scriptstyle \alpha $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\cos {\raise0.5ex\hbox{$\scriptstyle \alpha $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern 1pt} \!\lower0.7ex\hbox{$2$}}\frac{{k{h^2}b}}{{\sin \alpha }} \cong 0.69k{h^2}b\]
Taking the lower bound and the upper bound as limits, we therefore find
\[ \Rightarrow 0.5 \le \frac{M}{{k{h^2}b}} \le 0.69\]
This forms a good example of constraining the value of the external force between lower bound and upper bound. It is also a good example of how to produce a lower limit on an upper bound calculation.

