Thermodynamics of solid solutions
For an introduction to the basics of thermodynamics, look at the Phase Diagrams and Solidification TLP.
Entropy
The entropy of the two endmembers, A and B, of a solid solution are SA and SB, and are mainly vibrational in origin (i.e. related to the structural disorder caused by thermal vibrations of the atoms at finite temperature). The entropy of the solid solution will always be greater than the entropy of the mechanical mixture.
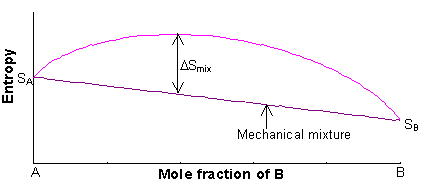
The entropy of the mechanical mixture is given by:
S = xASA + xBSB
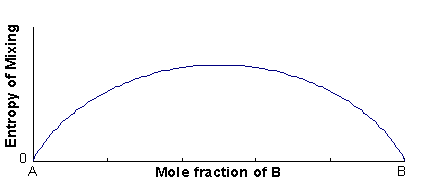
The excess entropy is called the entropy of mixing (ΔSmix), and is mainly configurational in origin (i.e. it is associated with the large number of energetically-equivalent ways of arranging atoms/ions on the available lattice sites).
The configurational entropy is defined as:
S = k lnW
where k is Boltzmann's constant (1.38 x 10-23 JK-1), and W is the number of possible configurations.
If it is assumed that the entropy of mixing is equal to the configurational entropy,
ΔSmix = k lnW
If we consider mixing NA A atoms and NB B atoms on N lattice sites at random, then the number of different configurations of A and B cations is given by:
\[w = \frac{{N!}}{{{N_A}!{N_B}!}} = \frac{{N!}}{{({x_A}N)!({x_B}N)!}}\]
where xA and xB are the mole fractions of A and B respectively.
Hence
\[\Delta {S_{{\rm{mix}}}} = k\ln \frac{{N!}}{{({x_A}N)!({x_B}N)!}} = k[\ln N! - \ln ({x_A}N)! - \ln ({x_B}N)!]\]
Stirling's approximation states that, for large N:
lnN! ≈ N lnN − N
Hence
ΔSmix = k(N lnN - N) - k(xAN lnxAN - xAN) - k(xBN lnxBN - xBN)
ΔSmix = -Nk(-lnN + 1 + xAlnxA + xAlnN - xA + xBlnxB + xBlnN - xB)
ΔSmix = -Nk(xAlnxA + xBlnxB + (xA + xB)lnN - (xA + xB) - lnN + 1)
Since xA + xB = 1,
ΔSmix = -Nk(xAlnxA + xBlnxB)
If N is taken to be equal to Avogadro's number, then per mole of sites:
ΔSmix = -R(xAlnxA + xBlnxB)
Enthalpy
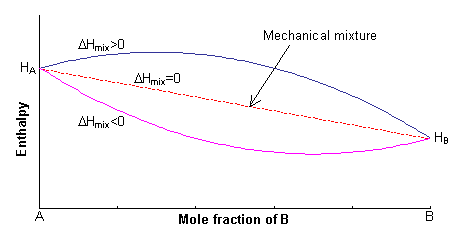
The enthalpy of the two endmembers of the solid solution, A and B, are equal to HA and HB respectively. For a mechanical mixture of these two endmembers, the enthalpy is given by:
H = xAHA + xBHB
The excess enthalpy relative to the mechanical mixture is known as the enthalpy of mixing, ΔHmix. This can either be positive or negative, or zero.
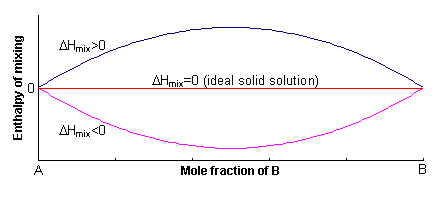
If ΔHmix = 0, the solution is said to be ideal, and for ΔHmix ≠ 0, the solid solution is said to be non-ideal.
A simple expression for the enthalpy of mixing can be derived by assuming that the energy of the solid solution arises only from the interaction between nearest-neighbour pairs.
Let z be the coordination number of the lattice sites on which mixing occurs. If the total number of sites is N, then the total number of nearest-neighbour bonds is 0.5Nz. (The factor of 0.5 arises since there are two atoms/ions per bond).
Let the energy associated with A-A, B-B and A-B nearest-neighbour pairs be WAA, WBB and WAB respectively. If the cations are mixed randomly, then the probability of A-A, B-B and A-B neighbours is xA2, xB2 and 2xAxB respectively.
Hence the total enthalpy of the solid solution is given by:
H = 0.5 Nz(xA2WAA + xB2WBB + 2xAxBWAB)
This can be rearranged to:
H = 0.5 Nz(xAWAA + xBWBB) + 0.5 NzxAxB(2WAB -WAA -WBB)
The first term in this expression is equal to the enthalpy of the mechanical mixture. Hence:
ΔH = 0.5 NzxAxB(2WAB -WAA -WBB) = 0.5 NzxAxBW
where W (= 2WAB -WAA -WBB) is known as the regular solution interaction parameter, and its sign determines the sign of ΔHmix.
A positive value of W indicates that it is energetically more favourable to have A-A and B-B neighbours, rather than A-B neighbours. In order to maximise the number of A-A and B-B neighbours, the solid solution unmixes into A-rich and B-rich regions. This process is called exsolution.
A negative value of W indicates that it is energetically more favourable to have A-B neighbours, rather than A-A or B-B neighbours. To maximise the number of A-B neighbours, the solid solution forms an ordered compound.
View a simple representation of exsolution and cation ordering

