Pourbaix diagrams and how they work

An electrochemical cell contains reactions as follows:

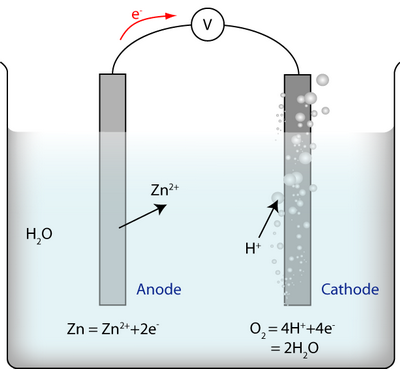
There are three reactions:

1. The reaction at the anode between metal ions and electrons
2. The reaction at the cathode between water and electrons
3. The reaction of the whole cell, i.e. the two half-cell reactions added together: \(2{\rm{Zn}} + {{\rm{O}}_2} + 4{{\rm{H}}^ + } = 2{\rm{Z}}{{\rm{n}}^{2 + }} + 2{{\rm{H}}_{\rm{2}}}{\rm{O}}\)

For each of these reactions it is true that:

$$\Delta G = \Delta {G^o} - RT\ln \left( {{{\prod\limits_X {a_X^{{n_X}}} } \over {\prod\limits_Y {a_Y^{{n_Y}}} }}} \right)$$

where:

ΔG is the free energy change of the reaction.
ΔG⁰ is what the free energy change would be if every component were in its standard state.
a_x is the activity of reaction product X  and  is the activity of reactant Y.
n_x is the stoichiometric coefficient of reaction product X, and likewise for the reactants.(The stoichiometric coefficient is the number of that molecule that are involved in the reaction; for the whole-cell reaction written above, the stoichiometric coefficient of water is 2, and of oxygen gas is 1.)
R is the ideal gas constant and T  is the temperature.
The symbol \(\Pi \) is the multiplying equivalent of \(\Sigma \) – all the terms after it are multiplied together.

Equilibrium

If a reaction is at equilibrium, \(\Delta G = 0\), and the free energy G of the system is at a minimum with respect to how much of the reactants have been converted to products. When this is the case, we obtain:

$$\left( {{{\prod\limits_X {a_X^{{n_X}}} } \over {\prod\limits_Y {a_Y^{{n_Y}}} }}} \right) = K$$

where K is the equilibrium constant.

Thus we can deduce that \(\Delta {G^o} = RT\ln K\); this is true of a reaction whether it is at equilibrium or not. (ΔG⁰ for a reaction is determined by the energies of the bonds within the molecules of the reactants and products, and this is independent of how many such molecules there are per unit volume.)

The cathode reaction is at equilibrium if there is no power supply connected to the circuit. It can do this because each atom or ion has enough energy to undergo the reaction in either direction; there is nothing stopping it being at equilibrium. The anode reaction is also at its own equilibrium.

The reaction for the whole cell is not at equilibrium. There is too much of an energy barrier for it to be able to get there – the ions have to diffuse through the electrolyte and the electrons have to go round the wires. (Or through a high impedance voltmeter, which they almost certainly cannot do.)

Thus for the example given

$$\Delta G = \Delta {G^o} - RT\ln \left( {{{{a_{Z{n^{2 + }}}}a_{H + }^2p_{{O_2}}^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}}} \over {{a_{Zn}}{a_{{H_2}O}}}}} \right)$$

ΔG⁰ ≠ 0 and the quotient is not the equilibrium constant.

We can convert this into an expression in electrical potentials using the general rule:

$$\Delta G = - zFE$$

where z is the stoichiometric number of electrons in the reaction. (This is due to Faraday’s law, of which more is given here.)

In this form we have the Nernst equation for the cell:

$${E_e} = {E^o} - {{RT} \over {zF}}\ln \left( {{{{a_{Z{n^{2 + }}}}a_{{H^ + }}^2p_{{O_2}}^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}}} \over {{a_{Zn}}{a_{{H_2}O}}}}} \right)$$

The activities of Zn and water are one, because Zn is in its standard state and the water is so much more abundant than its solutes that it may as well be in its standard state. Thus:

$${E_e} = {E^o} - {{RT} \over {zF}}\ln \left( {{a_{Z{n^{2 + }}}}a_{H + }^2p_{{O_2}}^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}}} \right)$$

E_e is the equilibrium potential – it is the potential of the whole cell when the electrodes are at equilibrium within themselves.

It can be worked out (easily, using algebra with a pen and pencil) that

$${E^o} = {{RT} \over {zF}}\ln K$$

where K is the equilibrium constant – i.e. if we were at equilibrium over the whole electrochemical cell, then E would be zero. E⁰ is a property of the system like ΔG⁰, and is still equal to the same number even when the whole cell is not at equilibrium. If for some reason it was required to find the value of E⁰, we could use this expression. E⁰ is called the standard electrode potential.

The Relevance of pH

The Nernst equation shows that the equilibrium potential is affected by the activity of hydrogen ions in the electrolyte. This means that the electrode potential must depend on the pH of the electrolyte. This can easily be found by using the relation:

$$pH = - \log \left[ {{{\rm{H}}^{\rm{ + }}}} \right]$$

Square brackets denote “concentration of \({{\rm{H}}^{\rm{ + }}}\)”. To make the Nernst equation in terms of concentrations so we can get it in terms of pH, we can express the quotient from the start in terms of concentrations and partial pressures instead of activities and partial pressures. (This implies that all the solutes in the electrolyte have the same relation between concentration and activity. That is not quite true but it is an adequate approximation in this case.)

Now, in every system, there is more than one possible reaction between the metal and its oxides and hydroxides, and the water. In the zinc system, for example, we have these possible reactions:

$$\eqalign{ & {\rm{Z}}{{\rm{n}}^{2 + }} + 2{e^ - } = {\rm{Zn \hspace{9.8em}(reaction\; i)}} \cr & {\rm{Zn(OH}}{{\rm{)}}_{\rm{2}}} + 2{{\rm{H}}^{\rm{ + }}} + 2{{\rm{e}}^{\rm{ - }}}{\rm{ }} = {\rm{ Zn}} + 2{{\rm{H}}_{\rm{2}}}{\rm{O \hspace{1.2em} (reaction\; ii)}} \cr & {\rm{HZn}}{{\rm{O}}_{\rm{2}}}^{\rm{ - }} + 3{{\rm{H}}^{\rm{ + }}} + 2{{\rm{e}}^{\rm{ - }}} = {\rm{Zn}} + 2{{\rm{H}}_{\rm{2}}}{\rm{O \hspace{1.4em} (reaction\; iii)}} \cr & {\rm{Zn}}{{\rm{O}}_{\rm{2}}}^{{\rm{2 - }}} + 4{{\rm{H}}^{\rm{ + }}} + 2{{\rm{e}}^{\rm{ - }}} = {\rm{Zn}} + 2{{\rm{H}}_{\rm{2}}}{\rm{O \hspace{1.7em} (reaction \;iv)}} \cr} $$

When we do the calculations, we find the Nernst equations for these reactions are:

$$\eqalign{ & {\rm{For\; reaction \;i: }}{E_e} = - 0.763 + 0.0295\log \left[ {Z{n^{2 + }}} \right] \cr & {\rm{For\; reaction\; ii: }}{E_e} = - 0.439 - 0.0591pH \cr & {\rm{For\; reaction\; iii: }}{E_e} = 0.054 - 0.0886pH + 0.0295\log \left[ {HZn{O_2}^ - } \right] \cr & {\rm{For\; reaction\; iv: }}{E_e} = 0.441 - 0.1182pH + 0.0295\log \left[ {Zn{O_2}^{2 - }} \right] \cr} $$

Now we can plot these as lines on a graph with pH on the horizontal axis and E_e on the vertical axis:

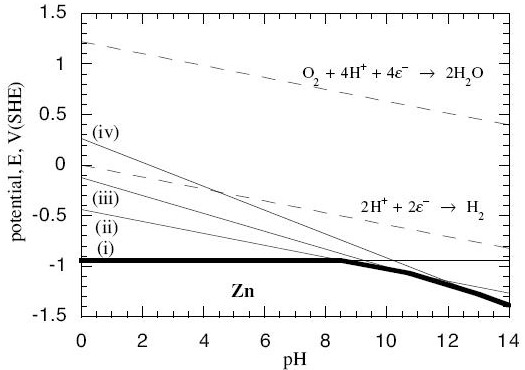(Contributed by G.T. Burstein, University of Cambridge.)

• The solid lines are the lines at which the anode reactions (i – iv) are at equilibrium within themselves. Off the lines, they are not at equilibrium.
• The dotted lines are equilibrium lines for reactions that water can undergo with oxygen and hydrogen, independently of the zinc.
  
• Below the bold line, all the reactions with Zn metal in them are pushed off equilibrium towards there being more solid Zn and less of the dissolved reactants on the other side of the reaction. No corrosion occurs below the bold line because it would be energetically unfavourable.