PreviousNext Scalars, Vectors and Matrices
Before we can move on to tensors, we must first be familiar with scalars, vectors and matrices. If you are comfortable with these concepts, you can move on to the next page.
Scalars
- These are direction independent quantities that can be fully described by a single number, and are unaffected by rotations or changes in co-ordinate system. Examples of physical properties that are scalars: Energy, Temperature, Mass.
- For this TLP scalars will be written in italics.
Vectors
- These are objects that possess a magnitude and a direction, and are referenced to a particular set of axes known as a basis. A basis is a set of unit vectors (vectors with a magnitude of 1) from which any other vector can be constructed by multiplication and addition.
- The vector is referenced to the basis by its components. If possible, the maths is simplified by using an orthonormal base with orthogonal (mutually perpendicular) unit vectors. Examples of physical properties that are described by vectors: Mechanical force, Heat flow, Electric field.
- Vectors will be written in bold and components of a vector, say x, will be written as xi
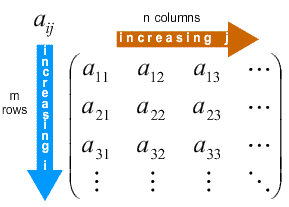
Matrices
- A matrix is a mathematical object that contains a rectangular array of numbers that can be added and multiplied (according to matrix multiplication rules). They are very useful in many applications, for example in reducing a set of linear equations into a single equation, storing the coefficients of linear transformations (e.g. rotations), and as we shall see, in describing tensors.
- The components of matrix A are written aij where i refers to the row element and j refers to the column element.
Scalar products
- For two vectors:
a = (a1, a2, a3) and b = (b1, b2, b3) The scalar product (also known as the dot product) is defined as: a.b = a1b1 + a2b2 + a3b3
and so, for example, the vectors (1, 4, −3) and (2, 5, 1) have a scalar product of 1×2 + 4×5 − 3×1 = 19.
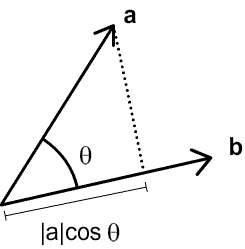
- The scalar product is related to θ, the angle between the two vectors, and can equivalently be written as: a.b = |a||b|cosθ.
- For vectors of unit length, we can see that the scalar product is equal to the cosine of the angle between them.
Matrix multiplication
If we have two matrices,
| A = |
| |
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
| |
|
and B = |
| |
| b11 | b12 | b13 |
| b21 | b22 | b23 |
| b31 | b32 | b33 |
| |
|
Then the product C = AB is found by ∑3k=1 aikbkj where i, j and k are indices that represent the position of the element in the matrix.
| C = AB = |
| |
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
| |
|
| |
| b11 |
b12 |
b13 |
| b21 | b22 | b23 |
| b31 | b32 | b33 |
| |
|
| = |
| |
| a11b11 + a12b21 + a13b31 |
a11b12 + a12b22 + a13b32 |
a11b13 + a12b23 + a13b33 |
| a21b11 + a22b21 + a23b31 |
a21b12 + a22b22 + a23b32 |
a21b13 + a22b23 + a23b33 |
| a31b11 + a32b21 + a33b31 |
a31b12 + a32b22 + a33b32 |
a31b13 + a32b23 + a33b33 |
| |
|
Don't bother trying to remember the above result, remember the rule:
ROW × COLUMN = RC = "Race Car" or "Really Cool!" or make up your own acronym to remember it. This is also useful to remember the conventional order of suffices, where the first suffix indicates the row and the second indicates the column.
You can use the following activity to practice more matrix multiplication.
3×3 determinants
The determinant of a 3×3 matrix can be calculated along any row by 'expanding by minors'. For the matrix
| A = |
| |
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
| |
|
The determinant is:
| |A| = |
| a11 | a12 | a13 |
| a21 | a22 | a23 |
| a31 | a32 | a33 |
|
|
= a11 |
|
- a12 |
|
+ a13 |
|
= a11(a22a33 - a23a32) - a12(a21a33 - a23a31) + a13(a21a32 - a22a31)
The minor of a11 is the 2×2 determinant made up from the elements not in its row or column. The minus sign appears because expanding along the rows or columns follows the cofactor pattern:
For more of a reminder about determinants see here.



