Thermodynamics - The Driving Force

The overall reaction in the cell can be described by two half-cell reactions: one for the anode and one for the cathode.

The cathodic reaction can be represented as:

, Standard electrode potential:

where a is the number of moles of A etc.

The cathode is usually a metallic oxide or a sulphide, but oxygen is also used.

The anodic reaction can be represented as:

, Standard electrode potential:

The anode is generally a metal, which is electrochemically oxidised to form a metal ion which is soluble in the electrolyte.

The anode and the cathode are connected internally through an electrolyte, which is an ionic conductor, thereby providing the medium for transfer of charge as ions between the two electrodes. It is typically a solvent containing dissolved salts, acids or bases. The electronic conduction in the electrolyte should be negligible in order to avoid self-discharge by internal short-circuiting.

The overall reaction is given by:

The change in standard free energy, , is given by:



where  is the standard cell potential

At conditions other than the standard state, E can be given as:



where (aC) is the activity of C etc.

This gives:

The change in of a reaction is the driving force for a battery, which enables it to deliver electrical energy.

Electrode Kinetics (polarisation and cell impedance)

Thermodynamics can tell us the feasibility of a cell reaction occurring, and the theoretical cell voltage, however it is necessary to consider kinetics to gain a better idea of what the actual cell voltage may be, since rates of charge transfer are usually the limiting factor.

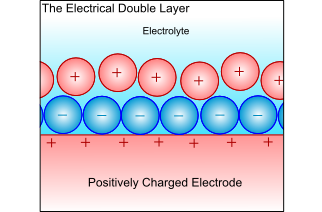
Electrical Double-Layer

When a metal electrode is in an electrolyte, the charge on the metal will attract ions of opposite charge in the electrolyte, and the dipoles in the solvent will align. This forms a layer of charge in both the metal and the electrolyte, called the electrical double layer. The electrochemical reactions take place in this layer, and all atoms or ions that ore to be reduced or oxidised must pass through this layer. Thus, the ability to pass through this layer controls the kinetics, and is therefore the limiting factor when controlling the electrochemical reaction.

Rate of reaction

The rates of the chemical reactions are governed by the Arrhenius relationship:
Rate of reaction:

where:

 is the activation energy for the reaction
T is the temperature in Kelvin
R is the universal gas constant

In this case, the rate of the reaction can be measured by the current produced, since current is the amount of charge produced per unit time, and therefore proportional to the number of electrons produced per unit amount of time; i.e. proportional to the rate.

Electrodes away from equilibrium

When an electrode is not at equilibrium an overpotential exists, given by

where η = overpotential, E = actual potential, E^o = equilibrium potential

The Tafel equation

Consider a general reaction for the oxidation of a metal at an anode:
M → M^z+ + ze^–

The rate of this reaction, k_a is governed by the Arrhenius relationship:

where K is the rate constant.

From Faraday’s law:

If an overpotential is now applied in the anodic direction, the activation energy of the reaction is reduced to , where α is the “symmetry factor” of the electrical double layer, usually 0.5.

Therefore

This is the Tafel equation.

By taking natural logs and rearranging, this can be written as:

Or, in terms of electrode potential,

, where b_a is the anodic Tafel slope.

Similarly, we can consider the reduction of metal ions at a cathode:

M^z+ + ze^– → M

The activation energy will be decreased by  giving:

and

Therefore

, where b_c is the cathodic Tafel slope.

The following is a typical Tafel plot – a plot of log i_o against E:

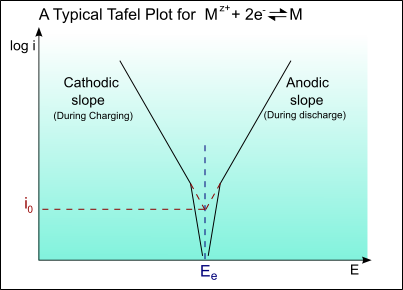
Thus for an applied potential, the current density can be found from the Tafel plot.

Example: Plotting Tafel curve of copper electrode.

Other limiting factors:

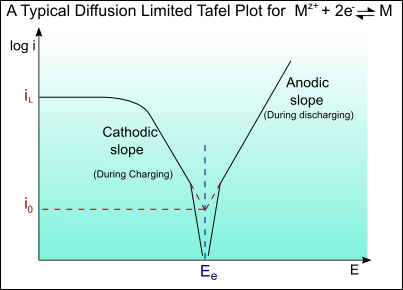
At very high currents, a limiting current may be reached as a result of concentration overpotential, η_C(conc).

where i_L is the limiting current (in this case for the cathodic double layer).

The limiting current is diffusion limited, and can be determined by Fick’s law of diffusion.

where:
D = diffusion coefficient of Cu²⁺ in the electrolyte
C = concentration of Cu²⁺ in the bulk electrolyte
δ = the thickness of the double layer

Typical values would be:
D = 2 × 10^-9 m²s^-1
C = 0.05 × 10⁴ kg m^-3
δ = 6 × 10^-4 m
which gives i_L = 3.2 × 10² A m^-2

A Tafel curve showing this diffusion limiting of the current is shown below:

Tafel curves for a battery

In a battery there are two sets of Tafel curves present, one for each material. During discharge one material will act as the anode and the other as the cathode. During charging the roles will be reversed. The actual potential difference between the two materials for a given current density can be found from the Tafel curve: The anodic potential, E_A, and cathodic potential, E_C, can be found from the curve. The total cell potential is the difference between the two.

On discharge, the potential is always less than thermodynamics alone predicts. It can be calculated by the equation:

Upon discharge the cell potential may be further deceased by the Ohmic drop due to the internal resistance of the cell, r. Thus the actual cell potential is given by:

where A = Geometric area relevant to the internal resistance.

Similarly on charging the potential is greater than thermodynamics alone predicts, and can be calculated by the equation:

The cell potential may now be increased by the Ohmic drop, and the actual cell potential is given by:

previous | next