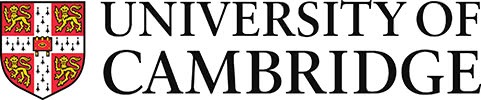Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Brittle Fracture Another way of calculating the energies
Brittle Fracture AimsBefore you startIntroductionWhen do atomic bonds break?Why do cracks weaken a material?Inglis and the crack tip stress ideaCan we calculate the energy changes?What about tension?Another way of expressing the energiesAnother way of calculating the energiesWhy bother if they are the same?Coping with a scatter in strengthSimulation of Weibull modulus experimentWhen does the sample fail completely?Sub-critical crack growth and R-curvesSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Another way of calculating the energies

Consider a crack growing from C by an amount δc to C'. Before cracking occurs there are stresses acting ahead of the crack and across the plane C − C'. After crack growth these stresses have been relaxed to zero as the newly created surfaces move from their initial position at u = 0 to form the crack.

Diagram of a crack growing

If we knew the stresses ahead of the crack and displacements that relaxed them to zero, we could estimate the total mechanical work, δUM, when the crack grows by δc.

What are the displacements, u?

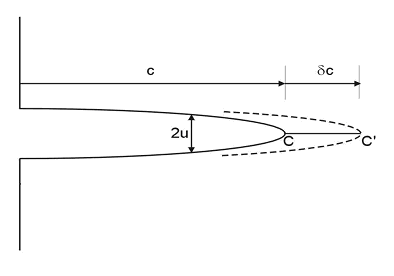
To find these we make a sharp cut in a rubber sheet, something compliant enough to get measurable shape changes without breaking, and stretch it, see below

We can plot the opening of the crack, u, against the distance from the crack-tip, r. Remember r is taken as positive ahead of the growing crack. The opening is therefore at negative values of r. From the picture

u ∝ −r½

where r is the distance from the crack tip, taken as positive in the direction ahead of the growing crack. The crack opening, u, at a given point is therefore at a negative value of r. A full elastic analysis gives

$$u = 4{K \over E}{\left( {{{ - r} \over {2\pi }}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern 0.1em} 2}}}$$

where K is a constant known as the stress intensity factor and E is the Young modulus.

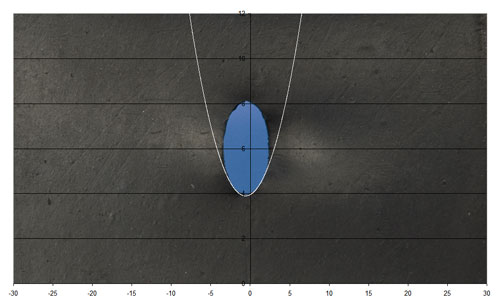
We can see this well by simply stressing a rubber sheet with a cut slit, the shape of the crack being clearly parabolic. A curve with equation

 y = m(x − a)2 + c can be fitted to the tip of the curve.

equation y=m(x-a)^2+c fitted to curve

What are the stresses ahead of a crack tip?

If the crack opening is parabolic, it seems not unreasonable to think that the stresses ahead of the crack (not at the crack tip) are too, so

$$\sigma = {K \over {{{\left( {2\pi r} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern 0.1em} 2}}}}}$$

We can reassure ourselves by carrying out a Finite Element simulation. Taking the expressions for u and σ and as the elastic energy is proportional to σ × u, we can see that the change in mechanical energy, δUM, is likely to be proportional to K2/E. To check we need to integrate δUM over the increment of crack growth δc. See here. As expected, this gives:

$$G = {{{K^2}} \over E}$$

Now, we said cracking occurred when G = R, an equivalent expression is

K = KC

where KC is the critical stress intensity factor at which the crack will grow, known as the fracture toughness. Both criteria are based on the idea that the mechanical energy per increment of crack growth must reach some critical value. Both are entirely equivalent and both calculate the energy changes on cracking.

PreviousNext