Derivation of γ
This small element of the wire subtends an angle dβ at the centre of the coil.
The shear strain produced by torsion is given by
\[\gamma = \frac{{{\rm{distance\; through\; which\; we\; twist}}}}{{{\rm{distance\; over\; which\; twist\; occurs}}}}\]
Which can be simplified, algebraically, to
\[\gamma = \frac{r}{2}{\theta _L}\]
where θL is the angular twist per unit length induced by the torque and r is the radial distance from the centre (\(0 \le r \le \frac{w}{2}\)).
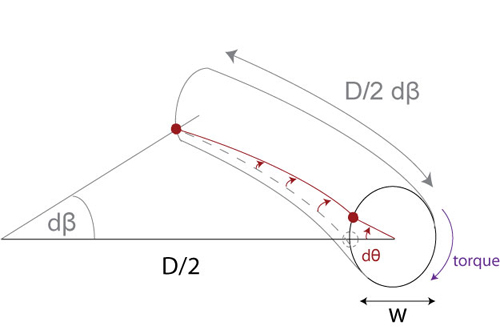
The torque acting on this element causes it to twist through an angle dθ.
Therefore, the twist per unit length is:
\[{\theta _{\rm{L}}} = \frac{{{\rm{d}}\theta }}{{(D/2){\rm{d}}\beta }}\]
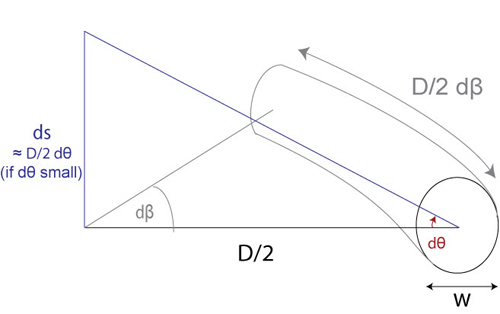
The vertical deflection of the coil due to the twisting of this element is:
\[{\rm{d}}s = \frac{D}{2}{\rm{d}}\theta = {\left( {\frac{D}{2}} \right)^2}{\theta _{\rm{L}}}{\rm{d}}\beta \]
The vertical deflection associated with the twist in one turn of the coil is:
\[s = \int_0^{2\pi } {{{\left( {\frac{D}{2}} \right)}^2}{\theta _{\rm{L}}}{\rm{d}}\beta = \frac{{\pi {D^2}}}{2}{\theta _{\rm{L}}}} \]
The peak local shear strain is thus given by:
\[{\gamma _{{\rm{max}}}} = \frac{{sw}}{{\pi {D^2}}}\]
It may be noted that the average local shear strain, γ, is proportional to the peak strain,
\[\gamma \propto \frac{{sw}}{{ {D^2}}}\]
As we did for the stress, we can note that D and w are control variables, and so simplify our expression to:
\[\gamma = Cs\]
where C is a constant for this experiment.

