Curie-Weiss law
Above a critical temperature Tc, the Curie temperature, all ferromagnetic materials become paramagnetic. This is because thermal energy is large enough to overcome the cooperative ordering of the magnetic moments.
The susceptibility of a material, χ, indicates how dramatically a material responds to an applied magnetic field, and is defined as the ratio of the magnetisation of the material, M, and the applied magnetic field, H.
\[\chi = \frac{M}{H}\;\;\;\;{\rm{equation}}\;1\]
The magnetisation of a material, M, is defined as the magnetic moment per unit volume or per unit mass of a material and is dependent on the individual magnetic dipole moments of the atoms in the material and on the interactions of these dipoles with each other.
Above the Curie Temperature there will be a change in the susceptibility as the material becomes paramagnetic, therefore giving the equation:
\[\chi = \frac{C}{{T - {T_c}}} = \frac{M}{H}\;\,\,\,{\rm{equation}}\;2\]
where C is a constant.
The graph below shows the saturation magnetisation (ie that obtained in a high magnetic field) of a ferromagnetic element, nickel, as a function of temperature. We see that the saturation magnetisation decreases with increasing temperature until it falls to zero at the Curie temperature where the material becomes paramagnetic:
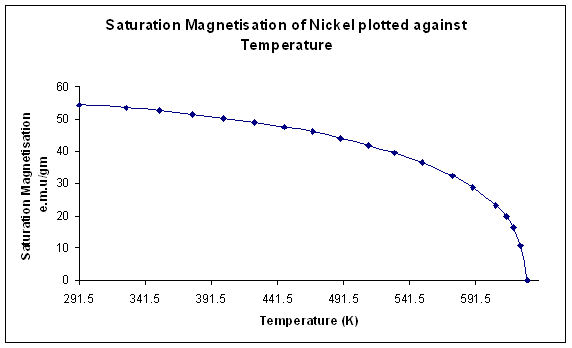
Figure J. Variation of saturation magnetisation with temperature for Nickel. (Data from Weiss and Forrer, 1926)
Differentiation of Equation 2 with respect to temperature shows that the susceptibility is a maximum at the Curie temperature. This is no surprise; it is easiest to increase the magnetic moment of the material by applying a magnetic field when the material is undergoing a transition between magnetic order and disorder. The graph below for nickel shows the susceptibility tending to infinity as the temperature moves closer to the Curie temperature:
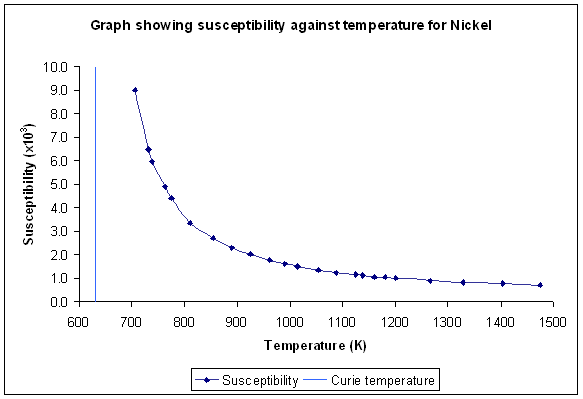
Figure K. Variation of susceptibility with temperature for Nickel (Sucksmith and Pearce, 1938)

