Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Mechanical Testing of Metals Indentation Hardness Measurement
Mechanical Testing of Metals AimsBefore you startIntroductionDeviatoric (von Mises) and Hydrostatic Stresses and StrainsTrue and Nominal Stresses and StrainsOverview of Plasticity and its Representation with Constitutive Laws Tensile Testing - Practical BasicsTensile Testing - Necking and FailureCompression Testing - Practical Basics, Friction & BarrellingIndentation Hardness MeasurementIndentation PlastometrySummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Indentation Hardness Measurement

Currently, most mechanical testing aimed at obtaining quantitative plasticity characteristics is carried out by uniaxial loading in tension or, to a lesser extent, in compression.  Tensile testing also provides a measure of the “failure strength” (in the form of an “ultimate tensile stress”) and the ductility.  However, these tests require relatively large (uniform) pieces of material, extensive machining to produce samples (at least for tensile testing), considerable care in the way that they are carried out and sound background knowledge in interpretation of the outcome (load-displacement data).  These represent substantial limitations and challenges.

A completely different approach, circumventing virtually all of these difficulties, is that of indentation.  This can be carried out on relatively small samples of simple shape  -  just a flat surface is required, can provide point-to-point mapping of plasticity characteristics over a surface and can be used for non-destructive field testing of components in situ.  It involves pushing a hard indenter into the surface with a known force and measuring the diameter of the resultant indent.  From this measurement, a “hardness number” is obtained.

The indenter must remain elastic  -  ie must experience no plastic deformation -  and is usually made of diamond or another very hard material.  There are several different types of hardness test, including those of Vickers, Brinell, Knoop and Rockwell.  They were all developed several decades ago and they essentially only differ in the shape (and in some cases the material) of the indenter.  A typical hardness test is that of Vickers, the geometry of which is shown below.  The (diamond) indenter is a right pyramid with a square base and an angle of 136˚ between opposite faces. 

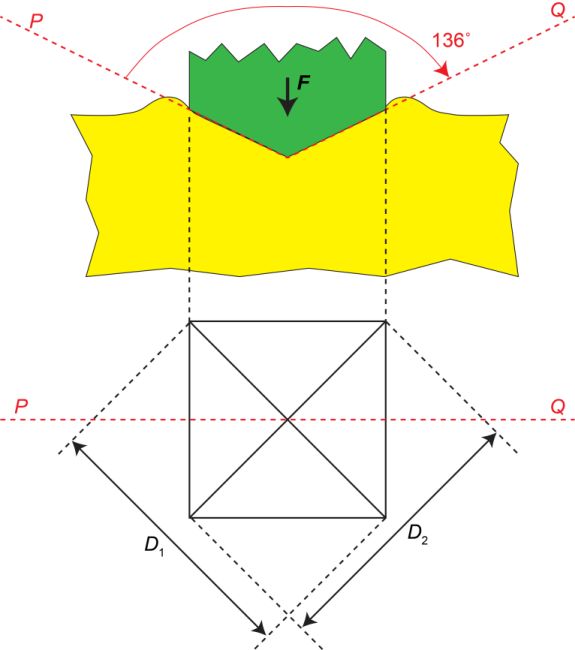
VIckers hardness test geometry

Geometry of the Vickers Hardness Test

The hardness number is the ratio of the applied force, in kgf, to the contact area (NOT the projected area), in mm2.  The measured indent diameter, D, taken as the average of D1 and D2, IS, however, measured in projection.  The value of HV is therefore given by

\[{H_{\rm{v}}} = \frac{{2F\sin \left( {\frac{{136}}{2}} \right)}}{{{D^2}}} = 1.854\frac{F}{{{D^2}}} \qquad \qquad \qquad \qquad (12) \]

so a simple calculation allows the hardness number to be obtained from the measured value of D.

There are, of course, certain assumptions incorporated into this analysis.  For example, elastic recovery of the specimen is neglected.  Furthermore, in practice the specimen may exhibit “pile-up” or “sink-in” around the indent, such that the true area of contact differs from that obtained via the simple geometrical picture above.

The stress acting on the contact area (in MPa) is obtained on multiplying the hardness number by 9.81.  However, to say the least, there is no simple relationship between this stress and the stress field generated in the material beneath the indenter.  The latter is complex and also depends in a complex way on the shape of the indenter and the plasticity characteristics of the material.  In fact, even for a given type of hardness, the number obtained tends to vary with the applied load.  This occurs because the load affects the level of plastic strain, which in turn dictates which portions of the stress-strain curve are affecting the outcome.

Nevertheless, it is in practice quite common to use simple expressions so as to obtain a yield stress value from a hardness number.  This is based on the fact that, in the absence of work hardening, and for a given indenter shape, there is an approximately linear relationship between the yield stress (which will be the von Mises stress throughout the volume that has plastically deformed) and the hardness number.  For the Vickers test

\[{\sigma _{\rm{\gamma }}} \approx \frac{{{H_{\rm{v}}}}}{3} \qquad \qquad \qquad \qquad (13) \]

Since very few materials exhibit no work hardening at all, a yield stress obtained in this way is not reliable.  In fact, it is likely to be indicative of a flow stress averaged in some way over the range of plastic strain experienced during the test, which depends on the depth of penetration, the indenter shape and the work hardening characteristics themselves.  It should never be regarded as more than a semi-quantitative indication of the resistance that the material offers to plastic deformation.

PreviousNext