Free energy

The free energy of mixing is defined as:

ΔG_mix = ΔH_mix - TΔS_mix

The variation in free energy as a function of composition and temperature can be considered for three different situations: an ideal solution, a non-ideal solution with a positive enthalpy of mixing, and a non-ideal solution with a negative enthalpy of mixing.

1. Ideal solid solution, ΔH_mix = 0

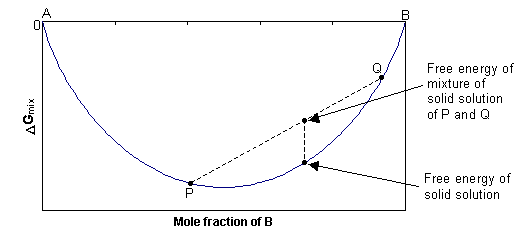
In this case, ΔG_mix = -TΔS_mix, and since ΔS_mix is always positive, ΔG_mix is always negative. At any composition, the free energy of the single-phase solid will be lower than the combined free energy of any mixture of the two separate phases, as shown in the diagram below. The solid solution is stable as a single phase, with disordered cation distribution at all compositions and temperatures.

2. Non-ideal solid solution, ΔH_mix > 0

At high temperatures, the -TΔS_mix term dominates, and the free energy curve resembles that of the ideal solution. As the temperature decreases, the ΔH_mix term and the -TΔS_mix term become similar in magnitude and the resulting free energy curve shows two minima and a central maximum.

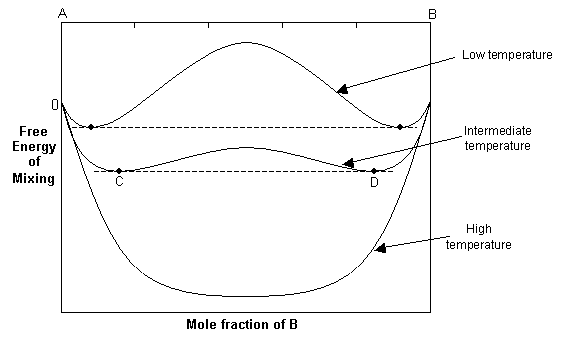
The common tangent rule can be used to determine the equilibrium state of the solid solution. The common tangent will touch the free energy curve at C and D, and for bulk compositions between these points, the free energy of the single-phase solution is higher than that of a mixture of C and D. Hence at equilibrium, the system will minimise its free energy by exsolving to two phases with compositions C and D. For compositions outside C and D, the solid solution will still be stable as a single phase since it has a lower free energy than a mixture of two phases.

3. Non-ideal solid solution, ΔH_mix < 0

In this case, there is a strong driving force for ordering when the A:B ratio is about 1:1. The fully-ordered phase has zero configurational entropy, because there are only two ways to arrange the atoms: the ordered and anti-ordered states (which are equivalent). However, this state has a low enthalpy, due to the energetically-favourable arrangement of ions, which stabilises the ordered phase at low temperatures. In contrast, the fully disordered solid solution has a high configurational entropy, which stabilises it at high temperatures. At a certain critical temperature, there will be a phase transition from the ordered to the disordered phase.