Interfacial debonding
Quick proof
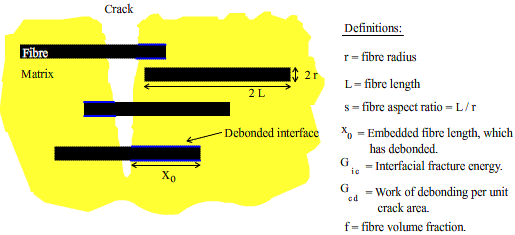
We need to start by considering short fibre composites as shown in the diagram above. The work done when a single fibre undergoes interfacial debonding is:
ΔW = 2 π r x0 Gic
Now we can sum this over all the fibres intersected by a unit area of the crack to find the work of debonding of the composite per unit crack area, Gcd. If there are N fibres per m2 where N is given by
\[N = \frac{f}{{\pi {r^2}_{^{}}}},\]
then there are ( N dx0 / L ) fibres per m2 with an embedded length between x0 and ( x0 + dx0 ).
\[{G_{cd}} = \int\limits_0^L {2\pi r{x_0}{G_{ic}}\frac{{Nd{x_0}}}{L}} \]
Integration gives: Gcd = f s Gic
This formula only applies to short fibre composites since fibre fracture does not occur if the fibre aspect ratio is less than the critical fibre aspect ratio, s* = σ f* / 2τ i*. (refer to TLP on short fibre composites, which does not exist yet). For long fibre composites there is a small probability that fibre fracture will occur away from the crack plane and debonding will not occur over the whole length of the fibre. In this case G>cd gives an idea of the magnitude of the energy absorbed.

