Defects
Just like regular crystal lattices, liquid crystals can contain defects these are given the name disclinations.
Normally liquid crystals are most stable when all of the molecules are aligned to point along a single director. However, external factors can force the direction of the director vector to change abruptly somewhere within the sample (such factors include external electric/magnetic fields or even the rigid sides of the container itself). Where this occurs the local director is said to be undefined, and the region in question is the disclination. The stability of a disclination is dependent on the Frank Free Energy of the liquid crystal – however discussion of this particular topic is beyond the scope of this TLP.
Some of the possible disclinations in a nematic liquid crystal are shown in the diagrams below (the dot indicates the location of the disclination itself whilst the lines represent the surrounding liquid crystal molecules and their orientations). Each type is assigned a number and a sign; the number indicates the strength of that particular disclination whilst the sign tells us which disclinations are capable of cancelling each other out should they come into contact (for example, the s = ½ and s = -½ disclinations could annihilate to produce a region with no defects).
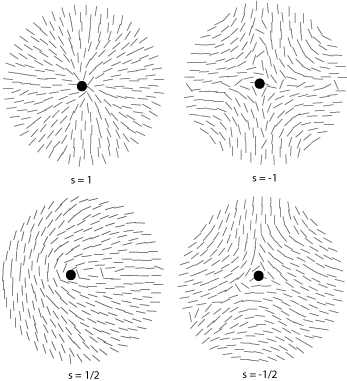
From the above diagrams we can therefore identify the disclination in the cover picture of this TLP as s = -1/2.
In actuality disclinations are 3-dimensional phenomena; the following 3D models are of s = 1 and s = -1 disclinations where the liquid crystal is constrained within a particular environment:
|
View an s = 1 point disclination (such as in a small spherical droplet) |
View an s = -1 point disclination (such as in a small spherical droplet) |
|
View an s = 1 line disclination (such as in a capillary tube) |
View an s = -1 line disclination (such as in a capillary tube) |
The concept of disclinations in liquid crystals is analogous to that of a dislocation in solid materials. The TLP Introduction to Dislocations covers this particular topic in more detail.